Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Let's begin the Transum Newsletter for the month of June 2024 with the puzzle of the month.
A judge is twice as old as her wig was when she was as old as her wig is now. How old are they now if the sum of their ages is 56?

If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email at: gro.musnarT@rettelsweN
While you think about that here are some of the key resources added to the Transum website during the last month:
Trig-Pythag Fusion is a brand new exercise requiring two (or three) distinct calculations. As the title suggests there may be a trigonometrical calculation required to find the second side of a right-angled triangle so that Pythagoras' theorem can be used to calculate the third. Or the other way round. Answers are marked instantly online though neatly set out working in exercise books is highly recommended.
Position Practice is a really basic activity requiring the use of words for position and direction including left, right, in front, behind, under and above. I've always found spatial awareness one of those things that pupils either deal with instinctively or really struggle to comprehend. The set of exercises is a prerequisite for problem-solving using Bearings and other more advanced topics for students that don't have this apparent intuition!.
Mix and Math has been updated (despite the missing s in the title) and provides a nice challenge for seconday students of any age. It's easy to cheat as there are only two possible answers to each question but your students are above that aren't they?
The Uniqueness Game was intended for whole-class use (projected on the whiteboard) but I have since found that it makes an excellent activity for online tutorials. I copy and paste the page into BitPaper and take it from there. Of course, there are no other solutions from 'the rest of the class', but earning an extra point if the student's answer is different from Captain Obvious' has been a great motivator.
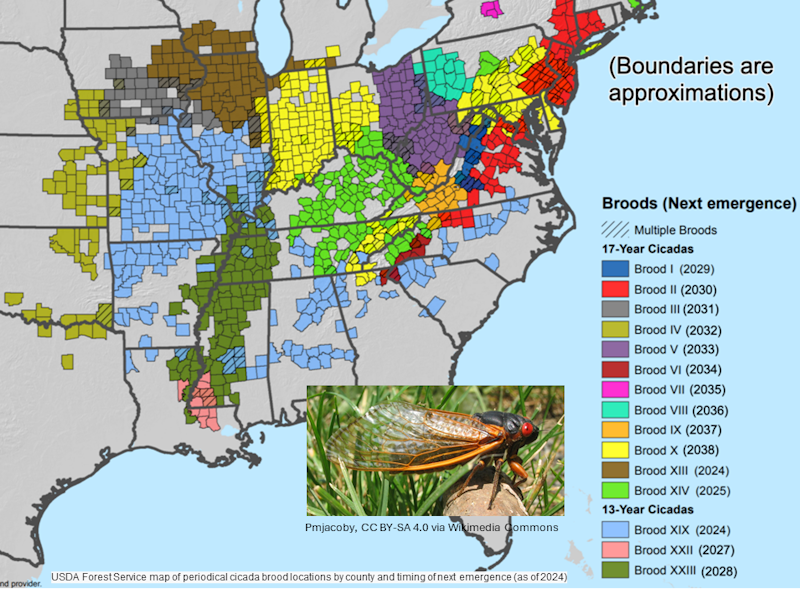
In my student days I worked my summers in America at Camp Tamarack in New Jersey. I remember in 1979 being surrounded by large colourful insects called cicadas which can only be seen every 17 years.
In 2024, Illinois is experiencing a rare natural spectacle: the simultaneous emergence of cicada Broods XIII and XIX. This event, first recorded in 1803, won’t occur again until 2245. These periodical cicadas, which emerge either every 13 or 17 years, spend the majority of their lives underground, only surfacing to reproduce at the end of their long developmental cycles.
After mating, females lay approximately 500 to 600 eggs in woody plants before the adults die, their life above ground lasting merely a month. The eggs hatch six weeks later, and the nymphs burrow into the soil to begin their 13 or 17-year cycle.
This synchronisation of 13 and 17-year cycles is a perfect natural example of common multiples. Have you been teaching LCM recently? This is a great, real-life example.
You've probably seen this video before even though it was only released a couple of weeks ago. It's the most impressive use of AI to teach Maths that I've ever seen. The future has arrived!
Last thing before sleeping I checked seven of the most popular weather sites to find out if it would rain in the morning when I wanted to take my early-morning cycle ride. They all gave a different percentage for the probability of rain. How can that be? The percentages ranged from 0% to 51%, quite a difference.
What do the percentages mean anyway?
I went on my ride, it did not rain and the sun peeped through the clouds! The percentage question remains unanswered in my mind.
Finally the answer to last month's puzzle which was:
I insist that members of my class bring certain items to the lesson. Today 90% remembered to bring a pen, 85% brought a pencil, 80% brought a calculator and 65% brought a ruler: what percentage, at least, must have brought all four items to the lesson?
The first five correct solutions were received from Kevin, Mala, Rick, Bardia and Shreyak.
Consider the percentages representing the students who forgot each item.
Given:
If we assume, pessimistically, that the students who forgot something are all different students, we sum these percentages to find the total percentage of students who forgot at least one item.The minimum percentage of students who brought all four items would then be whatever remains from 100% after subtracting the total percentage of students who forgot at least one item.
100% - ( 10% + 15% + 20% + 35% ) = 20%
At least 20% of the students must have brought all four items to the lesson: a pen, a pencil, a calculator, and a ruler.
That's all for now,
John
P.S. 15 + 15 is thirty
and,
16 + 16 is thirty too!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Rick Blaire, United States
Thursday, May 2, 2024
"Below is my answer to this month’s podcast puzzle:
90% brought a pen.
85% brought a pencil.
80% brought a calculator.
65% brought a ruler.
To determine what minimum percentage of students brought all items, let’s examine how many did not bring at least one item.
10% did not bring a pen.
15% did not bring a pencil.
20% did not bring a calculator.
35% did not bring a ruler.
If we assume these do not overlap, adding these percentages will be the maximum number of students that did not bring at least one item 80%). Thus, the remaining percentage is the minimum number of students (20%) that brought all four items to class. "