Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of November 2023 containing a rare opportunity to enjoy a unique Fibonacci Day. The date on the 10th, written as 10/11/23, represents a strange version of the Fibonacci sequence (each digit is the previous two added together).
If that's not exciting enough for you here's the puzzle of the month:
How many positive two-digit numbers are there whose square and cube both end in the same digit ?
Don't check them all ... come up with an efficient strategy and please let me know what it is. While you think about that here are some of the key resources added to the Transum website during the last month.
All For One is a new puzzle requiring you to create three fractions that combine with addition or subtraction to make 1. The idea for this puzzle came from Chris Smith's (@aap03102) wonderful weekly publication, the Grange Academy Newsletter. I created levels 1 to 4 only to get you ready for the big level five, which is quite difficult!
How Many of Each? has now got a new Level 2. I created Level 1 to match the National Curriculum statement "Pupils should be taught to find pairs of numbers that satisfy an equation with two unknowns". The new level extends that idea to three or more unknowns.
Divisibility Tests has been updated thanks to a prompt from Sharon who encourages students to click the Check button regularly, but notes an issue with this task where correct "non-responses" are prematurely marked as correct, suggesting a dedicated option for "not divisible by any". Her wish was my command and it has now been done.
The Triangle Solver has been updated and a message to students has been added: "... this tool is designed to enhance your understanding of trigonometry and to validate your calculations. While it can provide answers, solely relying on it for your homework bypasses the valuable learning process. We encourage you to first attempt your assignments independently, then use this app to verify your solutions. If discrepancies arise, consult with your teacher to bridge the gaps in your understanding. Remember, the journey of learning is as crucial as the destination."
ChatGPT now has eyes! Once again my experimenting with artificial intelligence has yielded impressive though not necessarily correct results. I was creating an exam-style question about a speed-time graph and I wanted to produce the graph in Desmos. I drew a rough sketch (below) of the shape I wanted and, here's the amazing bit, I uploaded it to ChatGPT and it could see my sketch!
I asked it if it could give me an equation that I could paste into a graph plotter to produce a nice looking version of the graph. It responded with:
Certainly! The graph you've provided appears to be a combination of linear and polynomial segments. While it might not be possible to exactly reproduce the curve using a single equation, I can offer a rough approximation using piecewise functions.
Here's a piecewise function that could roughly produce a similar shape:
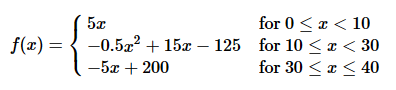
Well it was a bit of a fail as you can see below:
But there is a ray of hope, it made a reasonable attempt and I think in the future this could be something we might take for granted as the technology continues to develop.
Around the 5th November you can enjoy the Bonfire Night excitement in the classroom by using the Firewords starter, complete with sound effects. Despite it being a particularly popular Starter (if it ain't broke don't fix it) I have added clues for ten of the one pound words. I've positioned them on the page so that it is easy not to show them if your pupils need no help. After spending ten minutes on this Starter scroll right down the page to the Prime Words extension. That's wonderful!
Finally the answer to last month's puzzle which was: Write 1,000,000 as the product of two numbers; neither of which contains any zeros. The first five people to send me correct solutions were Martin Wright, Chris Smith, Ann Roberts, Allan Christie and Mikus Legzdins. Thank you, it was good to hear from you. I appreciate that.
Here's an elegant method for obtaining the unique solution:
1,000,000 can be written as 106.
10 is 2 x 5
So, the prime factorisation of 1,000,000 is 26 x 56
If a number has both 2 and 5 as factors, it will end in a zero. This is because 2 and 5 multiply to give 10, which introduces a zero at the end of the number.
Distribute the prime factors between two numbers such that neither number has both a 2 and a 5.
Number 1: Take all the 2's, which is 26.
Number 2: Take all the 5's, which is 56.
Calculate the two numbers.
Number 1: 26 = 64
Number 2: 56 = 15,625
Finally verify the solution by multiplying the two numbers to ensure they give 1,000,000.
64 x 15,625 = 1,000,000
Thus, 1,000,000 can be expressed as the product of 64 and 15,625, neither of which contains any zeros.
Finally I had an email from Rick Blair who said "I cheated and wrote a Python script to solve the problem".
That's all for now,
John
PS. I could tell you a joke about 288… But I won’t as it is two gross!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
