Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations.
Indices Pairs The traditional pairs or pelmanism game adapted to test knowledge of indices.
Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication.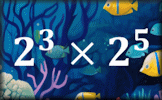
Power Play Exercises on powers and roots and simplifying index expressions involving numbers of the same base.
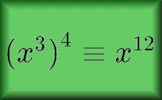Indices True False Arrange the given statements involving indices to show whether they are true or false.
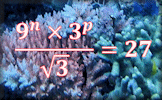Dr Tim's Indices Challenge Dr Tim Honeywill has come up with these challenges to test your understanding of indices and algebra.
Logarithms Self-marking exercises on evaluating logarithms and using them to solve equations.
Here are some exam-style questions on this statement:
- "(a) The \(n\)th term of a sequence is \(2^n+2^{n+1}\)" ... more
- "In an old science fiction book the author described the intensity of reverse polarity, \(P\) measured in treckons, is a function of the nebula thrust, \(N\) measures in whovians. The intensity level is given by the following formula." ... more
- "The following is an arithmetic sequence: \( \log_7 8 \text{, } \log_7 a \text{, } \log_7 b \text{, } \log_7 64 \) where \(a \gt 1 \text{ and } b \gt 1\)" ... more
Here are some Advanced Starters on this statement:
- Log Perfection
Determine whether the given statements containing logarithms are true or false more - Logarithm Equation
Solve an equation containing logarithms with different bases more - Product of Indices
Find the product of the unknown indices that feature in two equations more - Same Three Digits
Find expressions which contain indices and evaluate to numbers containing the same digits. more - Seventeen Camels
Explain the mathematics of the classic ninteenth century fraction sharing story. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Indices Where do many fish live? Indices (in the seas!) This topic involves the use of the index, power or exponent. The concept is easily misunderstood and a surprisingly large number of pupils will evaluate 62 as 12 and not 36. After having mastered positive integer indices pupils should move on to negative indices and fractional indices. Exploring this topic in both numeric and algebraic ways will provide understanding and competence in this important concept.
- Logarithms Older teachers will remember their school days, before calculators were widely available, using logarithms to perform difficult multiplication and division calculations. Nowadays logarithms, or logs as they are more commonly known, are studied as part of an A Level and International Baccalaureate course and are seen as being useful for solving certain exponential equations. Basically a logarithm is the inverse function to exponentiation.
Furthermore
The laws of exponents, also known as the rules of indices, provide a set of rules for simplifying expressions involving powers or exponents. When working with integer exponents, these laws help to manipulate and simplify algebraic expressions. The key formulae for the laws of exponents with integer exponents are as follows:
$$ a^m \times a^n = a^{m+n} \\ a^m \div a^n = a^{m-n} \\ (a^m)^n = a^{m \times n} \\ a^0 = 1 \quad (\text{where } a \neq 0) \\ a^{-n} = \frac{1}{a^n} \quad (\text{where } a \neq 0) $$
In the formulae above, \( a \) is the base and \( m \) and \( n \) are integer exponents.
Logarithms are a mathematical concept that provides a way to work with exponential equations in a more linear manner. The logarithm of a number to a given base is the power or exponent to which the base must be raised to produce that number. The most commonly used bases in logarithms are 10, often referred to as the common logarithm, and \( e \), the base of natural logarithms. The number \( e \) is an irrational number approximately equal to 2.71828 and has profound significance in mathematics, especially in calculus and complex analysis.
The key formulae for logarithms with base 10 and \( e \) are:
$$ \log_{10}(x) = y \quad \text{means} \quad 10^y = x \\ \log_e(x) = \ln(x) = y \quad \text{means} \quad e^y = x \\ \log_b(m \times n) = \log_b(m) + \log_b(n) \\ \log_b\left(\frac{m}{n}\right) = \log_b(m) - \log_b(n) \\ \log_b(m^n) = n \times \log_b(m) $$
This video on Exponential and Logarithmic Functions is from Revision Village and is aimed at students taking the IB Maths AA Standard level course.
This video on Log Laws and Solving Equations is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
