Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Transformations Video A demonstration of the four basic transformations: reflection, translation, rotation and enlargement.
Transformations Video A demonstration of the four basic transformations: reflection, translation, rotation and enlargement. Vector Maze Use vectors to navigate through a maze by the shortest distance.
Vector Maze Use vectors to navigate through a maze by the shortest distance. Vector Connections Video Learn how coordinates can be linked with vectors and how these vectors can help you decide if three points are collinear.
Vector Connections Video Learn how coordinates can be linked with vectors and how these vectors can help you decide if three points are collinear.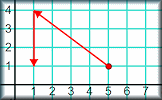 Vector Connectors Exercises about vectors and coordinates; using one to find the other.
Vector Connectors Exercises about vectors and coordinates; using one to find the other. Transformations Draw transformations online and have them instantly checked. Includes reflections, translations, rotations and enlargements.
Transformations Draw transformations online and have them instantly checked. Includes reflections, translations, rotations and enlargements. Vector Cops Help the cops catch the robbers by finding the vectors that will end the chase.
Vector Cops Help the cops catch the robbers by finding the vectors that will end the chase.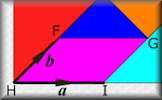 Vectors An online exercise on addition and subtraction of vectors, multiplication of vectors by a scalar, and diagrammatic representations of vectors.
Vectors An online exercise on addition and subtraction of vectors, multiplication of vectors by a scalar, and diagrammatic representations of vectors.
Here are some exam-style questions on this statement:
- "OABC is a parallelogram with O as origin. The position vector of A is \(a\) and the position vector of C is \(c\)." ... more
- "(a) Shape \(A\) is translated to shape \(B\) using the vector \( \begin{pmatrix}m\\n\\ \end{pmatrix}\). What are the values of \(m\) and \(n\)?" ... more
- "ABCD is a quadrilateral. The points E, F, G and H are the midpoints of the sides of this quadrilateral." ... more
- "In the parallelogram OABC two of the sides can be represented by vectors \(a\) and \(c\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Transformations A transformation in mathematics is an operation performed on a shape (or points) which changes the view of that shape (or points). This topic includes four transformations namely reflection, translation, rotations and enlargement. A reflection can best be described as the mirror image of a shape in a given line (which acts as the mirror). After reflection the shape remains the same size but the orientation is the mirror image of the original. The transformation known as a translation can be thought of as a movement or shift in position. The size and orientation of the shape remains the same but the position on the plane changes. A rotation can be described as turning. This transformation is defined by the angle of turning and the centre of rotation (the point which does not move during the turning). Finally enlargement is the term we use when a shape increases in size but maintains the same shape. The shape after enlargement is defines as being similar to the shape before enlargement. His use of the word similar has a precise mathematical meaning. All of the angles in the enlarged shape are the same as the angles in the original shape and the lengths of the sides are in the same proportion. An enlargement is defines by the scale factor of the enlargement and the centre of enlargement. We use the term enlargement even if the shape becomes smaller (a scale factor between minus one and one). A negative scale factor will produce an enlarged mirror image of the original shape.
- Vectors Vectors usually first make an appearance when pupils learn about transformations. A translation is best described with a vector written as a two by one matrix. Following that pupils learn how vectors can be used to prove geometric relationships in simple line diagrams. Ultimately vectors are studied as a major topic for A Level and International Baccalaureate courses where vectors in three dimensions are included.You can think of a vector as what is needed to 'carry' the point A to the point B. The Latin word vector means ‘carrier’ and was first used by 18th century astronomers investigating planet rotation around the Sun.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

