
 |
Exam-Style Questions on Normal DistributionProblems on Normal Distribution adapted from questions set in previous Mathematics exams. |
1. | IB Studies |
The heights of palm trees along a beach are normally distributed with a mean of 4.55m and a standard deviation of 0.37m.
(a) Find the probability that a randomly chosen tree has a height greater than 4.55m.
(b) Find the probability that a randomly chosen tree will be within 2 standard deviations of the mean. Give your answer as an integer percentage.
(c) Use your graphic display calculator to calculate the probability that a randomly chosen tree will have a height greater than 4m.
(d) The probability that a particular tree is less than \(x\) metres tall is 0.75. Find the value of \(x\).
2. | IB Studies |
A group of students sat a Biology examination and a Computer Studies examination. The students' marks in the Biology examination are normally distributed with a mean of 70 and a standard deviation of 9.
(a) Draw a diagram that shows this information.
(b) Find the probability that a randomly chosen student who sat the Biology examination scored at most 70 marks.
Eric scored 82 marks in the Biology examination.
(c) Find the probability that a randomly chosen student who sat the Biology examination scored more than Eric.
The students' marks in the Computer Studies examination are normally distributed with a mean of 68 and a standard deviation of 11. Eric also scored 82 marks in the Computer Studies examination.
(d) Find the probability that a randomly chosen candidate who sat the Computer Studies examination scored less than Eric.
(e) Determine whether Eric's Computer Studies mark, compared to the other students, is better than his mark in Biology. Give a reason for your answer.
To obtain a grade A a student must be in the top 12% of the students who sat the Computer Studies examination.
(f) Find the minimum possible mark to obtain a grade A. Give your answer correct to the nearest integer.
3. | IB Analysis and Approaches |
In particular atmospheric conditions the diameters of snowflakes \( X \) are normally distributed with a mean (?) of 3 mm and standard deviation (?): 0.5 mm.
The random variable \( X \) is normally distributed with mean 10 and standard deviation 2.
(a) Find the probability that \( X \) is more than 2 standard deviations above the mean.
The probability that \( X \) is more than \( k \) mm is 0.1, where \( k \in \mathbb{R} \).
(b) Find the value of \( k \).

4. | IB Analysis and Approaches |
The time in minutes taken to drive through a city at different times of the day can be modelled by a normal distribution with mean of 45 and standard deviation of 12. A commuter will be late for work if it takes more than an hour to drive through the city.
(a) Find the probability that the commuter is late for work.
(b) Estimate the number of days on which the commuter was late from random sample of 100 days.
(c) Given that the commuter is not late, find the probability that the cross-city journey took less than 25 minutes.
5. | IB Standard |
A random variable \(X\) is normally distributed with \(\mu=250\) and \(\sigma=25\).
Find the interquartile range of \(X\).
6. | IB Standard |
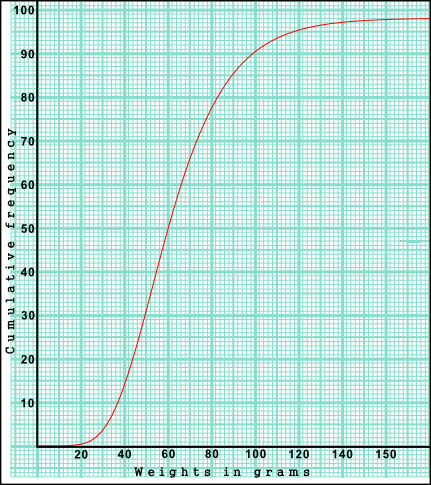
The weights in grams of 98 mice are shown in the cumulative frequency diagram. The heaviest mouse weighted 160g.
(a) Write down the median weight of the mice.
(b) Find the percentage of mice that weigh 70 grams or less.
The same data is presented in the following table.
| Weights w grams | 0 < w ≤ 40 | 40 < w ≤ 80 | 80 < w ≤ 120 | 120 < w ≤ 160 |
|---|---|---|---|---|
| Frequency | p | 63 | q | 3 |
(c) Find the value of p.
(d) Find the value of q.
(e) Use the values from the table to estimate the mean and standard deviation of the weights.
A second batch of mice are normally distributed with the same mean and standard deviation as those of the first group mentioned above.
(f) Find the percentage of the second batch of mice that weigh 70 grams or less.
(g) A sample of five mice is chosen at random from the second batch. Find the probability that at most three mice weigh 70 grams or less.
7. | IB Analysis and Approaches |
The travelling times by train, \( T \) minutes, between two towns can be modelled by a normal distribution with a mean of 55 minutes and a standard deviation of \( \sigma \) minutes.

(a) Given that 8% of the times are longer than 68 minutes, find the value of \( \sigma \).
(b) Find the probability that a randomly selected train journey will have a duration of more than 75 minutes.
(c) Given that a train journey between the two towns takes longer than an hour, find the probability that it takes less than 70 minutes.
On a particular day, there are 42 trains scheduled to travel between these two towns.
(d) Find the expected number of train journeys that will have a duration of more than an hour.
(e) Find the probability that more than 10 of the journeys on this particular day will have a duration of more than one hour.
8. | IB Standard |
The weights of players in a sports league are normally distributed with a mean of 75.2 kg, (correct to three significant figures). It is known that 75% of the players have weights between 67 kg and 80 kg. The probability that a player weighs less than 67 kg is 0.05.
(a) Find the probability that a player weighs more than 80 kg.
(b) Write down the standardized value, z, for 67 kg.
(c) Hence, find the standard deviation of weights.
To take part in a tournament, a player's weight must be within 1.5 standard deviations of the mean.
(d) Find the set of all possible weights of players that take part in the tournament.
(e) A player is selected at random. Find the probability that the player takes part in the tournament.
Of the players in the league, 22% are women. Of the women, 60% take part in the tournament.
(f) Given that a player selected at random takes part in the tournament, find the probability that the selected player is a woman.
9. | IB Standard |
Eels are elongated fish, ranging in length from 5cm to 4m. In a certain lake the length of the eels are normally distributed with a mean of 84cm and a standard deviation of 18cm. Eels are classified as giant eels if they are more than 120 cm long.

An eel is selected at random from the lake.
(a) Find the probability that this eel is a giant.
(b) Given that this eel is a giant, find the probability that it is longer than 130cm.
(c) Two eels are selected at random. Find the probability that they are both giants.
100 eels are selected at random.
(d) Find the expected number of these eels that are giants.
(e) Find the probability that at least 5 of these eels are giants.
10. | IB Analysis and Approaches |
The length, \(X\) minutes , of a certain category of online video is normally distributed with a mean of 28.
The probability that \(X\) is less than 20 is 0.213.
(a) Find \(P(20 \lt X \lt 28)\).
(b) Find the standard deviation of \(X\).
(c) Hence, find the probability that a video selected at random from this category lasts longer than 33 minutes
A random sample of 12 videos from this category are downloaded.
(d) How many of these videos could be expected to last longer than 33 minutes?
(e) Find the probability that exactly two of these videos last longer than 33 minutes.
(f) A video selected at random from the complete online collection of videos in this category has a running time of less than 20 minutes. Find the probability that its length is between ten and fifteen minutes.
11. | IB Analysis and Approaches |
The random variable X follows a normal distribution with mean \(\mu\) and standard deviation \(\sigma\).
(a) Find \( P(\mu - 1.25\sigma \lt X \lt \mu + 1.25\sigma) \).
The pineapples grown on a farm in Thailand have weights, in grams, that are normally distributed with mean \(\mu\) and standard deviation \(\sigma\). Pineapples are categorised as tiny, regular, super or giant, according to their weight. The following table shows the probability a pineapple grown on the farm is classified tiny, regular, super or giant.
| Size | Tiny | Regular | Super | Giant |
|---|---|---|---|---|
| Probability | 0.08 | 0.72 | 0.16 | 0.04 |
The maximum weight of a tiny pineapple is 895 grams.
The minimum weight of a giant pineapple is 1804 grams.
(b) Find the values of \(\mu\) and \(\sigma\).
One season a wholesaler purchased all the regular, super and giant pineapples from the farm.
Find the probability that a pineapple chosen at random from this purchase is categorized as
(c) regular.
(d) super.
(e) giant.
The wholesaler sells the pineapples at the following prices:
| Size | Regular | Super | Giant |
|---|---|---|---|
| Price | 40 ฿ | 60 ฿ | 80 ฿ |
The wholesaler pays the farm 8000 ฿ for the pineapples and assumes it will then sell them in exactly the same proportion as purchased from the farm.
(f) Find the minimum number of pineapples that must be sold so that the net profit for the supermarket is at least 4000 ฿.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.