
 |
Exam-Style Questions on ExponentialProblems on Exponential adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher [132] |
Richard studies fish populations in a lake.
The size of a certain fish population at the start of 2015 was 3700.
The size of this fish population increases exponentially.
Richard assumes that the rate of increase is 15% per year.
(a) Using his assumption, work out the size of this fish population at the start of 2010.
(b) Richard’s assumption is too high. Explain how your answer to part (a) is affected.
2. | IB Studies [85] |
While studying a new disease, scientists found that the number of toxic cells in the bloodstream increased over time, according to the model \(D(t)=12×(1.16)^t , t \ge 0\) where \(D\) is the number of the toxic cells in the bloodstream per litre and \(t\) is the time in hours.
(a) Find the number of toxic cells in the bloodstream at \(t=0\).
(b) Calculate the number of toxic cells in the bloodstream after 3 hours.
(c) Determine the time it takes for the number of toxic cells in the bloodstream to first exceed to 200 per litre. Give your answer to the nearest minute.
3. | IB Standard [78] |
Percy Cod and Fran Finklestein are both researchers working at different universities. They are each studying a different colony of bacteria which coincidentally start increasing in size at the same time.
The number of bacteria in Percy's colony, after \(t\) hours, is modelled by the function \(P(t)=8e^{0.3t}\).
(a) Find the initial number of bacteria in Percy's colony.
(b) Find the number of bacteria in Percy's colony after four hours.
(c) How long does it take for the number of bacteria in Percy's colony to reach 350?
The number of bacteria in Fran's colony, after t hours, is modelled by the function \(F(t)=16e^{kt}\).
(d) After four hours, there are 35 bacteria in Fran's colony. Find the value of \(k\).
(e) The number of bacteria in Percy's colony first exceeds the number of bacteria in Fran's colony after \(n\) hours, where \(n\in \mathbb Z\). Find the value of \(n\).
4. | IGCSE Extended [121] |
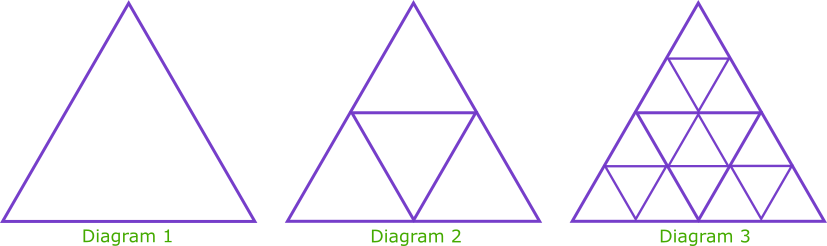
The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre.
In the second diagram there are four triangles each with sides of length \(\frac{1}{2}\) metre.
In the third diagram there are 16 triangles each with sides of length \(\frac{1}{4}\) metre.
(a) Complete this table for more diagrams.
| Diagram 1 | Diagram 2 | Diagram 3 | Diagram 4 | Diagram 5 | Diagram 6 | Diagram \(n\) | ||
| Length of Side | 1 | \(\frac{1}{2}\) | \(\frac{1}{4}\) | |||||
| Power of 2 | 20 | 2-1 | 2-2 |
(b) Complete this table for the number of the smallest triangles in diagrams 4, 5 and 6.
| Diagram 1 | Diagram 2 | Diagram 3 | Diagram 4 | Diagram 5 | Diagram 6 | Diagram \(n\) | ||
| Number of smallest triangles | 1 | 4 | 16 | |||||
| Power of 2 | 20 | 22 | 24 |
(c) Calculate the number of the smallest triangles in the diagram where the smallest triangles have sides of length \(\frac{1}{256}\) metre.
5. | GCSE Higher [136] |
The quantity of heat required to heat an amount of water is given by the formula:
$$H = atI^2 – b$$Where \(H\) is the number of calories delivered by an electric current of \(I\) amps acting for \(t\) seconds and \(a\) and \(b\) are constants.
(a) Rearrange the formula to make \(I\) the subject.
The graph below gives information about the cooling of a cup of coffee on a cold day. The vertical axes shows the variation in the temperature, \(T\), and the horizontal axis shows the time, \(t\), in seconds.
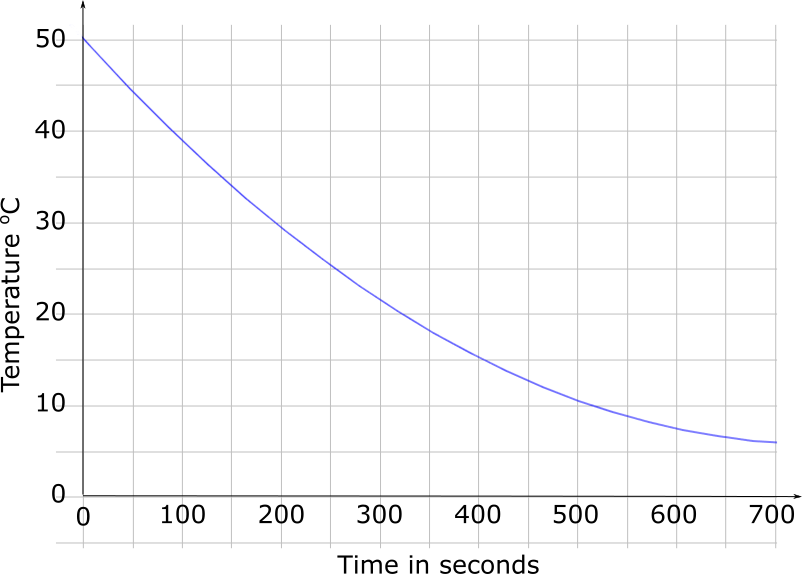
(b) Work out the average rate of decrease of the temperature of the coffee between \(t = 0\) and \(t = 700\).
The instantaneous rate of decrease of the temperature of the water at time \(A\) seconds is equal to the average rate of decrease of the temperature of the water between \(t = 0\) and \(t = 700\).
(c) Find an estimate for the value of \(A\) showing how you got your answer.
6. | IB Applications and Interpretation [434] |
Doctor Octothorpe investigated the decreasing population of a colony of ants in a remote province of China. His investigation took place in 1958.
He found that during the summer season their population, \(P\), could be modelled by the exponential equation
$$P = 560 + 9560(1.3)^{-t} \quad \text{where} \quad t \ge 0$$where \(t\) is the number of days into the season (\(t = 1\) represents the beginning of 1st June).
(a) Find the population of the ants at the beginning of 31st May 1958.
(b) Find the population of the ants at the beginning of 10th June.
(c) Calculate the date when the population first fell below 1000.
(d) According to this model, find the smallest possible population of ants.
7. | IB Analysis and Approaches [710] |
Find the range of possible values of \(a\) such that \(5e^x - \ln{a} = e^{2x}\) has at least one real solution.
8. | IB Analysis and Approaches [692] |
In medical imaging, the radioactive isotope Technetium-99m is used due to its short half-life of 6 hours. After being introduced into the body, the isotope decays, and the amount of Technetium-99m present can be tracked over time to study the function of specific organs.
The amount, \( A \), of Technetium-99m present in a patient's body \( t \) hours after injection can be modelled by the equation $$ A = A_0e^{-kt} $$ where \( t \geq 0 \) , \(A_0 \) and \( k \) are positive constants.
At the time of injection, the patient is defined to have 1000 units of Technetium-99m.
(a) Show that \( A_0 = 1000 \).
The time taken for half the original amount of Technetium-99m to decay is known to be 6 hours.
(b) Show that $$ k = \frac{\ln 2}{6} $$.
(c) Medical guidelines suggest that a scan should be performed when the activity of Technetium-99m is between 25% to 50% of the initial dose to obtain a clear image. Calculate the time window after the injection during which the scans should be performed.
9. | IB Studies [209] |
A cup of hot tea is placed on a table to cool. The temperature of the room is 24oC.
This situation can be modelled by the exponential function:
$$T = a + b (k^{-m})$$where \(T\) is the temperature of the water, in oC, and \(m\) is the number of minutes for which the cup has been placed on the table.
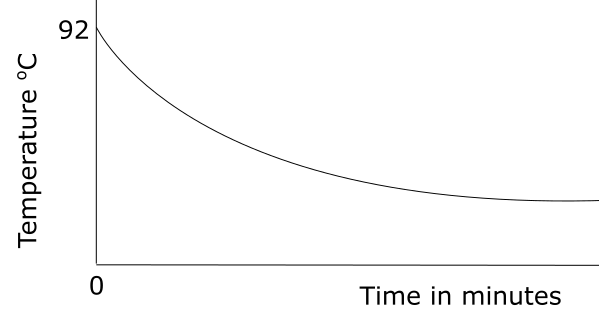
(a) Find the value of \(a\)
Initially the temperature of the tea is 92oC.
(b) Find the value of b.
After one minute, the temperature of the tea is 74oC.
(c) Find the value of \(k\).
(d) Find the temperature of the tea three minutes after it has been placed on the table.
(e) Find the total time needed for the tea to reach a temperature ofof 30oC. Give your answer in minutes and seconds, correct to the nearest second.
10. | A-Level [392] |
In a remote lake it was noticed by conservationists that a disease was rapidly spreading amongst two species of fish, R and S, which is reducing their numbers. The conservationists calculated that the numbers of each type of fish can be modelled by the functions:
$$ r(t) = 9000e^{-\frac{1}{10}t} $$and
$$ s(t) = 6000e^{-\frac{1}{20}t} $$respectively where t is the time in weeks after the disease was first detected on the 2nd August 2019.
(a) Use the two models to find the number of species R and S on 2nd August 2019.
(b) Find the number of species S after 24 weeks from 2nd August 2019, giving your answer to the nearest 10.
(c) After how many whole weeks will the number of species R first fall below 4500?
(d) Use logarithms and the two models to calculate the value of t when the number of species S will be three times that of species R. Give your answer to the nearest whole number.
(e) When \(t = T\) the number of species \(S\) first exceeds that of species R by 500. Use this information and the two models to derive a quadratic equation in \(x\) where:
$$ x=e^{-\frac{1}{20}T} $$(f) Hence find the number of days after 2nd August 2019 when this difference of 500 fish will first occur. Give your answer to the nearest day.
11. | IB Standard [373] |
Fifty milligrams of a certain type of medicine has been shown to enter the bloodstream of an adult according to the following equations:
where \(t\) is measured in minutes and \( t\ge 0 \)
(a) State the initial rate at which the medicine enters the bloodstream.
(b) Calculate the time it takes before the rate at which the medicine enters the bloodstream is halved.
(c) Find the rate of the medicine entering the bloodstream when there is 25 mg present in the bloodstream.
(d) Sketch both R and A on the same axes. Indicate clearly any intercepts and the equations of the horizontal asymptotes.
(e) Will the patient ever feel the full effect of the 50-milligram dose?
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.