These are the topics related to the standard: Solve real-life and mathematical problems involving angle measure, area, surface area, and volume."
Here are some specific activities, investigations or visual aids picked out. Click anywhere in the grey area to access the resource.
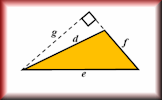 Area and Perimeter Show that you know the area and perimeter formulas of basic shapes.
Area and Perimeter Show that you know the area and perimeter formulas of basic shapes. Area And Perimeter Video Calculate and solve problems involving perimeter and area of rectangles, triangles, parallelograms, trapezia, kites and composite shapes.
Area And Perimeter Video Calculate and solve problems involving perimeter and area of rectangles, triangles, parallelograms, trapezia, kites and composite shapes.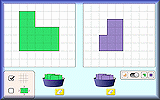 Area Builder An interactive workspace in which to make shapes using square tiles with given areas and perimeters.
Area Builder An interactive workspace in which to make shapes using square tiles with given areas and perimeters.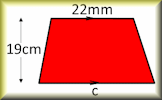 Area of a Trapezium Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.
Area of a Trapezium Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.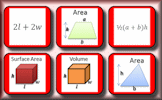 Formulae Pairs Find the matching pairs of diagrams and formulae for basic geometrical shapes.
Formulae Pairs Find the matching pairs of diagrams and formulae for basic geometrical shapes. Measuring Angles Measure the size of the given angles to within two degrees of their actual value.
Measuring Angles Measure the size of the given angles to within two degrees of their actual value. Scale Drawings Measure line segments and angles in geometric figures, including interpreting scale drawings.
Scale Drawings Measure line segments and angles in geometric figures, including interpreting scale drawings. Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Surface Area Work out the surface areas of common solid shapes in this collection of exercises. Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae. Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids. Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Here is an exam-style questions on this statement:
Click on a topic below for suggested lesson starters, resources and activities from Transum.
- Angles Pupils should understand that angles represent an amount of turning and be able to estimate the size of angle. When constructing models and drawing pupils should be able to measure and draw angles to the nearest degree and use appropriate language associated with angles. Pupils should know the angle sums of polygons and that of angles at a point and on a straight line. They will learn about angles made in circles by chords, radii and tangents and recognise the relationships between them. Pupils will work with angles using trigonometry, transformations and bearings. In exams pupils are often instructed that while non-exact answers should be given to three significant figures, angle answers should be given to one decimal place.
- Area Pupils should not only be able to remember and apply area formulae but they should also have a good understanding of what area means. This can be achieved by beginning the study of area with plenty of practical examples. The Pin Board provides an open-ended interactive experimental environment to secure a good fundamental understanding of area. Some examinations provide formulae sheets but it is still important that pupils know the common formulas for finding the areas of basic shapes. They should use these formulae in context to find areas of basic and compound shapes and be able to give answers using appropriate units. Pupils will also learn to find the surface areas of three dimensional shapes, use scale to determine areas from maps and solve real world problems involving areas. See also the topics called Measures, Shape (3D) and Ratio.
- Bearings A bearing is a description of a direction. It is the number of degrees measured in a clockwise direction from north as seen from above. Convention, probably born out of the need to be quite clear when saying a bearing over a crackly aircraft radio or storm at sea, three figures are given for each bearing. So 90 degrees would be expressed as 090 degrees. The four main directions are known as the cardinal points. These are north (360°), east (090°), south (180°) and west (270°). The directions in between those are known as the half cardinal points and can be expressed as north-east (045°), south-east (135°), south-west (225°) and north west (315°). The study of bearings in Mathematics provides a practical, real-life application of angles and geometry. It can provide a need for numerical calculations, scale drawing and estimation.
- Circles This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation. Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations. More mathematics related to the circle can involve angle theorems, loci and algebra.

