If the base of this triangle became 8cm but the other sides remained 5cm, how much would its area increase?
Topics: Starter | Area | Mensuration | Problem Solving | Pythagoras
How did you use this starter? Can you suggest
how teachers could present or develop this resource? Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for Maths teachers anywhere in the world.
Click here to enter your comments.
Previous Day | This starter is for 5 August | Next Day
Sign in to your Transum subscription account to see the answers
Can you find another pair of triangles that, like those above, surprisingly have the same areas?
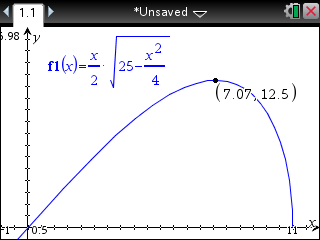
What is the length of the base which gives the triangle mentioned above the maximum area?
|
Change the background of this page to
or
for clearer classroom display.
|
||

|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=August5 However it would be better to assign one of the student interactive activities below. |
|
Here is the URL which will take them to a related student activity.
A first thought might be that the graph of area against length of base is symetrical but it is not. A graphic calculator will help you identify equal-area bases and the length of base giving the maximum area: