Kite Maths
Introduction
Explore Geometry With Kites!
Can you make a kite shape from a single A4 size sheet of paper using only three folds? Click Here to find out how.
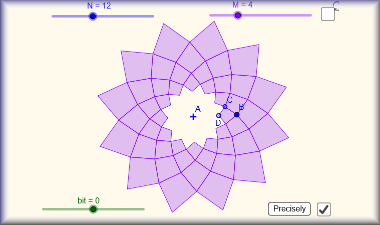
Will your kite tessellate? Can you put a number of kites together to make a symmetric design? What about 4 lines of symmetry and rotational symmetry of order 8.... is it possible?
Can you write a procedure in Logo to draw a kite .... what designs can you make with your Logo kites?
What is a kite?
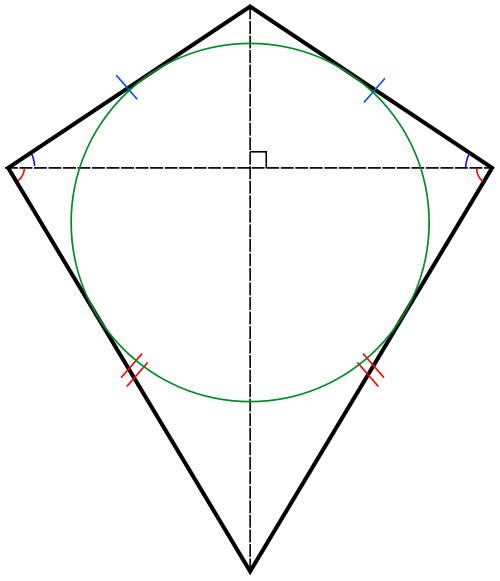
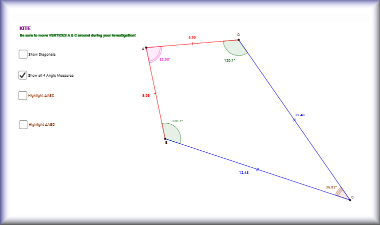
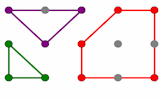
In geometry a kite, sometimes known as a deltoid, is a quadrilateral with two disjoint pairs of congruent adjacent sides. A kite can also be described as a quadrilateral with an axis of symmetry along one of its diagonals.
A kite, as defined above, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead".
Kite Facts
- A kite can be a geometrical shape (a special quadrilateral) and a toy that flies in the wind.
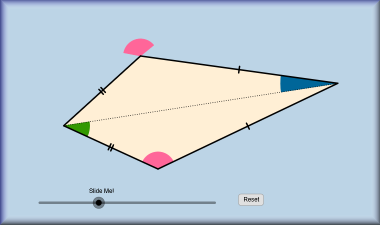
- A kite is a quadrilateral with two pairs of adjacent sides that are equal in length.
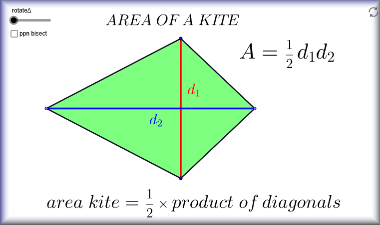
- The diagonals of a kite are perpendicular to each other.
- One of the diagonals of a kite bisects the other diagonal.
- If a kite has all four sides are of equal length then it is a rhombus.
- The angle at which a kite flies relative to the ground is called the "angle of elevation."
- The length of the string from the person to the kite can be used, along with the angle of elevation, to calculate the height of the kite using trigonometry.
- The tension in the kite string is a result of the balance between the gravitational force pulling the kite downwards and the aerodynamic lift and drag forces.
- The kite's tail helps stabilize it by adding drag, preventing excessive spinning or tumbling.
- In addition to fact number 1, a kite can also be the common name for a number of birds of prey.
Instructions
Fold an A4 sheet of paper to make a kite!
 |
 |
| Step 1 | Step 2 |
 |
 |
| Step 3 | Step 4 |
Activities
Challenges and investigations with Kites!
- Activity 1
- Fold a kite from an A4 sheet of paper by following the given instructions. What type of symmetry does your kite have?
- Activity 2
- Make seven more kites from sheets of A4 paper. Put your eight kites together to make different patterns. Can you work out the interior angles of the kite from the ways they fit together?
- Activity 3
- Make a kite from an A5 sheet of paper (half an A4 sheet). Will the smaller kite be half the width of the first kite you made? half the area? Will it's angles be the same?
- Activity 4
- Can you put a number of kites together to make a symmetric design with 4 lines of symmetry and rotational symmetry of order 8? Is it possible?
- Activity 5
- Use a computer program such as Logo or Geogebra to create patterns with kites.
- Activity 6
- You can fold an A4 sheet of paper to make a pentagon too. Click here to find out how.
Other Shape Activities
Logo
Use a computer to draw kites!
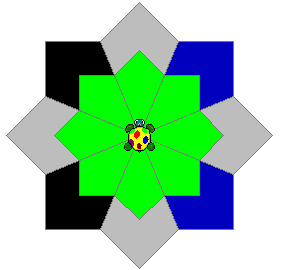
Here is a Year 8 student's design
to kite
:size
lt 22.5
fd :size * 1.85
rt 67.50
fd :size
rt 90
fd :size
rt 67.5
fd :size * 1.85
rt 157.5
pu
fd 10
fill
bk 10
pd
end
to design
setfillcolor 7
kite 55 rt 45
setfillcolor 1
kite 55 rt 45
setfillcolor 7
kite 55 rt 45
setfillcolor 1
kite 55 rt 45
setfillcolor 7
kite 55 rt 45
setfillcolor 0
kite 55 rt 45
setfillcolor 7
kite 55 rt 45
setfillcolor 0
kite 55 rt 45
setfillcolor 10
repeat 8 [kite 35 rt 45]
end
Here are some more designs made with Logo
There is no time like the present! Click the button below and draw your first kite using Online Logo:
ONLINE LOGODisplay
Colourful kites make great displays!

Click on an image below to see the full size animation. | |
 |
 |
 |
 |
It may take a while for Geogebra animations to load.






Lina Anagnos, Greece
Saturday, June 1, 2013
"I think that you could extend the activity by giving a kite constructed at a geogebra or Sketchpad file. It would be important for the students to connect the meanings of kite's area with the meaning of the diagonals. Another aim is the understanding of the shape reflections."
Transum,
Tuesday, October 25, 2016
"Thanks Lina for the suggestion. A Geogebra page has now been added so that you can interact with the kites and learn about their properties."
Jack Bradley, England
Thursday, February 14, 2019
"Vey good Transum."