Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More

Merry Christmas to one and all! This is the Transum Newsletter for the month of December 2025 and it brings you a traditional, festive puzzle of the month.
Two elves, Holly and Mistle, are helping to fill a magical toy sack for Santa. Working together, they can fill the sack in 22.5 minutes. The quicker elf could fill the sack all by their 'self', 24 minutes faster than the slower elf.

How many minutes would it take each elf to fill the toy sack on their own?
If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Fire off an email to: gro.musnarT@rettelsweN
Many of the activities on the website have been updated during November and, in preparation for the festive season, the ChristMaths collection has been brightly polished.
The first door of the Maths Advent Calendar is now unlocked!
I created the ChristMaths activities because, for many people in the Western world, Christmas is associated with warmth, happiness and positive memories. Shops, hotels and restaurants use this seasonal atmosphere to encourage people to engage with what they offer, and I see no reason why maths teachers cannot do the same. While there is research suggesting that some decorative images can distract from the main learning, I believe that carefully chosen visuals and colour schemes can instead create a friendly, welcoming environment. If a Christmas theme helps to soften the fear or dislike some students feel towards mathematics, and encourages them to see it as something enjoyable and approachable, then that can only be a good thing.
Merry Modulo Match is a festive board game that lets students practise using the modulo operation (finding the remainder after division). Players spin a wheel to get a number, then choose to divide it by 3, 5, or 7, with the remainder determining how many spaces their piece moves. This turns an abstract mathematical concept into a strategic decision-making game. Modulo is fundamental in computer programming, cryptography and problem-solving. The game works well for pairs or small groups and reinforces mental arithmetic whilst making this important concept accessible and engaging.
Treasure Hunt has a Christmas theme. This clue generator allows you to print posters to place around your school, containing mathematical clues to the next location. It can make a fun activity for your last Maths lesson before the Christmas holiday.

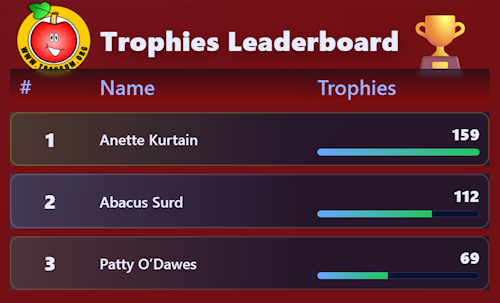
Subscriber Maria wrote to me saying "I always give out certificates to the learners who have earned the most trophies over the year." Maria went on to explain that she had difficulty knowing which trophies had been earned during this past year and which trophies were from previous years. In order to solve this problem, I created the leaderboard feature. Go to the page where you see the trophies earned by members of your class. Scroll right down to the bottom, and you’ll see a new button called "Open Leaderboard". You can set the "date since" to be the start of your school year. Clicking the button will reveal a list of students ranked by the number of trophies they have earned. It is designed so that it can be projected in front of the whole class, but I would strongly suggest that you only show the top three or maybe five students and leave the bottom of the list hidden below the visible area. Note that trophies expire after three years.
Don't forget that you can listen to this month's podcast, which is the audio version of this newsletter. You can find it here, on Spotify or on Apple Podcasts. You can follow Transum on BlueSky, Twitter (some call it X) and 'like' Transum on Facebook.
Snow Angles must be the only activity on the Transum website that was created to match the clever title. I was amused by the fact that it is very easy to misread the words angels and angles, so I thought an exercise needed to be written to match the title. The objective is to estimate the size of the angles marked in the snow angels. There's a generous tolerance level when the system marks the students' answers.
Finally, the answer to last month's puzzle, which was:
Three friends, Attika, Burt and Celia, are having a rock, paper, scissors competition. They play two at a time with the third person spectating. The winner stays on, and the loser becomes the spectator. There are no draws. At the end of the day, they summarise the number of matches each has played:
Who lost the second match?
Solution: Attika lost the second match. You can see a variety of creative solutions in the comments section below. I'm really interested to see the thought processes of people who have given time to solving the Puzzle of the Month. Thank you all so much.
The puzzle is adapted from Adrián Paenza's Brainy Miscellany, and was seen in the Guardian newspaper on 9 June 2025.
That's all for now. I wish you a very Happy Christmas and a wonderful New Year!
John
P.S. Deck the halls with boughs of holly, Fa (La)9…
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Chris, Scotland
Saturday, November 1, 2025
"With the players having each appeared 10+15+17 =42 times there must have been 21 matches. Poor Attika is awful at this game because even the worst rock-paper-scissors player in this system gets to play every second game. That means if she was in the very first match she would have racked up a minimum of 11 games (even if they were losses). So she must have lost 10 times and spectated 11 times. That means Burt and Celia played the first and last match, with Attika getting beaten in every even round match. So Attika lost game two!"
Stephen, Reddit
Wednesday, November 5, 2025
"In total, the kids were involved in a match 42 times. So there were 21 matches, giving rise to 21 wins and 21 losses. The most significant constraint comes from Attika being in only 10 of those matches. This means that at least 11 matches must have been between Burt and Celia.
Whenever Burt plays Celia, the winner then must play against Attika. So after each of the 11 B-C matches, someone will play Attika. But Attika was in only 10 matches, which means that one of the B-C matches has to have happened at the very end. The only way this lines up is with Attika playing in each of the even matches, while Burt and Celia face off in each of the odd matches.
If Attika were to win any of her matches, she would be in the next match as well, but we figured out that all odd numbered matches are B-C. So, Attika must lose all her matches, and in particular she must lose the second match of the day.
Note: in the picture, we see that the girl on the left is winning the match, so this must be Celia. Attika is cheering in the back, her spirit unbroken by her string of losses. (Or perhaps they're only just starting.)."
Refreshing Username, Reddit
Thursday, November 6, 2025
"Alternate, slightly simpler route to the solution:
The sum of matches played between the players is 42, so with 2 players in each match there were 21 matches. You play, at a minimum, in every other match because the spectator replaces the loser. The sole way to play in only 10 matches is to lose every even numbered match (2, 4, 6, ... 18, 20). Therefore, Attika played in and lost the 2nd match."
Rick, United States
Tuesday, November 11, 2025
"The sum of all the matches played by the three participants is 10 + 15+ 17 = 42. Two participants are required per match, so there were 21 matches. Since Attika played in 10 matches, that means that they did not play in 11 matches. The only way this is possible is if Attika sat out each odd numbered match and played in each even number match. However, Attika could not be the winner of the second match, since that would mean they would not sit out match three. Therefore, Attika lost the second match."