Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Gill, Leighton Buzzard
Monday, October 6, 2025
"Firstly - I love Transum- keeping students engaged with all your hard work makes my life so much more pleasant in the classroom.
This puzzle was a little tricky for my Year 7s - although they made some interesting expressions and connections with the \(N\)s!!
However some smarter ones in Y8 (we are a middle school so only go up to Y8, although we teach Y9/Y10 content to our more able) at our drop in maths clinic (yes it's a thing, and yes it's well turned out) came up with this:
If there are \(N\) trees, \(N\) nests and \(N\) eggs then the total number of eggs is \(N \times N \times N \equiv N^3 \). The snake eats \(N\) eggs so there are \(N^3 - N\) eggs left.
(after a lot of experimentation and a couple of suggestions) - they factorised to get
\(N(N^2-1) \equiv N(N-1) (N+1)\) ; figuring that \(N-1, N \text{ and } N+1\) must be consecutive numbers, (at least) one must be even (divisible by 2) and another must be a multiple of 3 (divisible by 3) which means that they must be divisible by 6 - hence there cannot be any remainder and the children can guard the eggs evenly.
I was quite impressed with the collaboration / wider thinking even when they went off down a rabbit (snake) hole! Keep them coming! "
Rick, USA
Friday, October 10, 2025
"
I really enjoyed this puzzle. Here is the full answer to the October puzzle of the month:
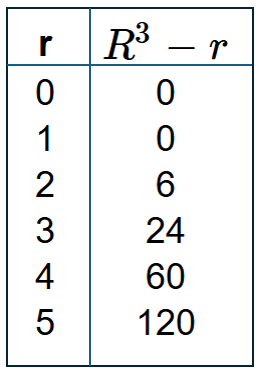
Since there are N trees, N nests in each tree, and N eggs in each nest, we start with \(N^3\) eggs. From this, we need to subtract N eggs, since that is how many were eaten by the snake. Therefore:
$$\text{Eggs} = N^3 - N$$
N can also be represented as (x+r), where x is the value of the integer division of N by the number of children and r is the remainder. Therefore:
$$\text{Eggs} = (x+r)^3 - (x+r) \text{ or}$$
$$\text{Eggs} = x^3 + 3x^2r + 3xr^2 + r^3 - x - r$$
Since we are only concerned with the remainder of the division of eggs by the number of children, we can eliminate any term with x, since x is evenly divisible by the number of children, leaving:
$$\text{Eggs remainder} = r^3 - r$$
There are only six children, so let's check what the remainder would be for the six values of r (0 to 5). See the following table:
We can see that the values in the second column of the table are all evenly divisible by six, so the remainder, regardless of the value of N, will always be zero. Hence, the remaining eggs can be evenly distributed among the six children, with no extra eggs.
"