Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Here's another Transum Newsletter. This one is for the month of July 2025 and it begins, as usual, with the puzzle of the month.
A rectangle is drawn inside a right-angled triangle. One vertex of the rectangle coincides with the triangle's right angle. Another of the rectangle's vertices meets the triangle's hypotenuse. The rectangle is 34mm from one of the acute angles and 25mm from the other. What is the area of the rectangle?
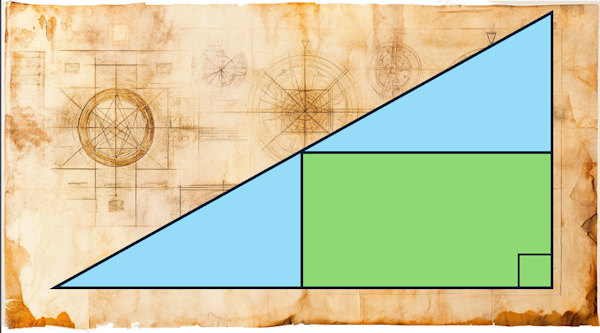
If you get an answer I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email at: gro.musnarT@rettelsweN
While you think about that here are some of the key resources added to the Transum website during the last month.
Stalactites is a quick two-player maths game in which pupils race to “grow” the longest stalactite by choosing numbered "growths" from a shared pool. Each turn belongs to the player whose stalactite is currently shorter: they keep adding numbers until they match or exceed their opponent’s height, at which point play passes over. Because the lead can change hands at any moment, the game stays tense right up to the final piece and encourages thoughtful decision-making. Is it better to overtake by a little or a lot? Along the way pupils gain fluent practice in mental addition, comparing totals and estimating differences, while experiencing a beautifully balanced catch-up mechanism that models fairness in competitive situations. It takes only minutes to learn, needs minimal equipment, and makes an engaging starter or plenary that blends strategic thinking with essential number skills.
Angle Aim is a retro game intended to provide light relief after students have completed the four levels of Estimating Angles. Meteorites fall from the sky and the idea is to quickly type in an angle between 1 and 180 degrees as an angle of extended elevation for the cannon to shoot the meteorites before they hit the ground. Lots of fun.
Polygon Profiles is a brand-new visual aid that shines a spotlight on the properties of regular polygons. Project it full-screen on your whiteboard and show the class polygons from a triangle all the way up to an icosagon, revealing (or hiding, at the click of a toggle button) each shape's interior and exterior angles, lines of symmetry and order of rotational symmetry. It's ideal for quick-fire questioning, spotting patterns and nipping common misconceptions in the bud. Pupils can predict the facts before you unveil them, then check their answers in real time.
I can’t remember exactly what inspired me to create the Semaphore Quiz, but one Friday I found myself completely engrossed in programming the rotating flags. The quiz has eleven levels, each with six questions, and the messages are sent a little faster as you progress through the levels. While not explicitly mathematical, the quiz incorporates several mathematical concepts, from the angles of the flags to the logical structure of the code. The great codebreakers throughout history were brilliant mathematicians for a reason!
Last month I added a brand‑new Level 5 to the Area Maze puzzles. Whether or not you can read Japanese, this will provide a suitable challenge for your high attainers. Building on the first four levels, this sophisticated variation invites students to unravel intricate rectangle-based diagrams by calculating missing lengths using only whole number arithmetic. Inspired by Japanese logic‑puzzle tradition, it demands careful reasoning and deep understanding of the rectangle area formula. Level 5 introduces more complex layouts and subtly deceptive rectangle groupings, perfect for those ready to think outside the box.
There are some notable dates in July:
For schools in the Northern Hemisphere, the end of the academic year is rapidly approaching. What do you do with your Maths classes during that very last lesson of term?
I'd really love to know what you get up to ... as long as it's Maths-related. I’m a bit of a stickler for not wanting to waste time (mathematically speaking), but I do believe the last lesson should still be memorable, exciting, and fun. Here is my life-long collection of ideas, brought together on the End of Term Maths page.
Interesting Stories Maths teachers can tell...
From the Roman era (2nd to 4th centuries AD), archaeologists have unearthed over a hundred hollow bronze objects now called Roman dodecahedrons. Each has 12 pentagonal faces pierced by circular holes of varying sizes and small knobs at each vertex. Found across Britain, France, Germany and Hungary, but never in Rome itself, their true function remains a tantalising mystery. Theories range from ritual or magical items and surveying instruments to knitting aids, calendrical devices or measures for pipes and shafts.

Gallo-Roman Museum, CC0, via Wikimedia Commons
When teaching about the platonic solids, these dodecahedrons offer a real-world example that blends mathematical elegance with historical mystery. Fascinating!
Finally the answer to last month's puzzle which was:
A rectangular jigsaw puzzle has 864 pieces. The number of pieces along its length and width have a lowest common multiple that is six times their highest common factor. How many pieces of the puzzle do not have any straight edges?
I began with the prime factorisation of 864. My scientific calculator did this for me quickly, though the manual methods wouldn’t have taken much longer.
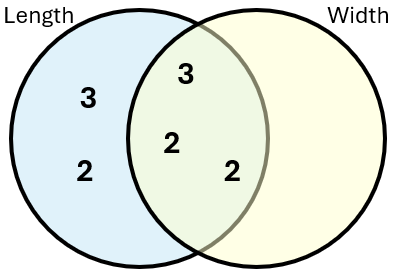
I drew a two-set intersecting Venn diagram representing the length and the width (and I assumed that the length was the longer of the two). I did this because the product of the numbers in the intersection of the two circles represents the highest common factor, and the product of the numbers in the union of the two circles represents the lowest common multiple. We are told that the lowest common multiple of the two numbers is six times as big as the highest common factor, so the numbers in the circles outside the intersection must multiply together to give 6.
For one solution, I put the number 3 in the left part of the diagram and the number 2 in the right part. Half of the remaining factors go into the intersection (because the intersection will be counted twice when multiplying together to get the area or total number of jigsaw pieces).

Hence the length and the width can be found by multiplying the factors in each of the circles, giving 36 and 24 as the dimensions.
The other solution is found by putting the 2 and 3 both in the same region on the left of the Venn diagram. This gives a length and width of 72 and 12.
Therefore, the number of pieces with no straight sides is 748 (if the puzzle dimensions are 36 × 24), or 700 if the dimensions are 72 × 12. A common mistake was to count the corner pieces twice when removing the pieces with straight edges.
Not everyone got the answer correctly on their first attempt nevertheless, I was delighted to receive the emails about the puzzle. The first five people to get in touch were Kevin, Chris, Mala, Allan and Esther.
That's all for now,
John
P.S. What did the coordinates do at the greengrocer's?
Ordered pears.
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Chris, Scotland
Sunday, June 1, 2025
"1. It reminded me of a jigsaw puzzle I posed during lockdown:
2. I learned this morning that in excel you can find the Lowest Common Multiple Function (=LCM) and Greatest Common Divisor (=GCD) function in Excel using these simple built in functions.
3. Having broken down 864 into its prime factors it's easy to write its 24 factors. That gives us the 24 pairs of possible sidelengths.
4. We could do this without it, but I'm excited to use the LCM, GCD formulaes so rush back to excel now. to discover a 36x24 jigsaw has sidelengths with LCM 72 and HCF of 12 (the LCM is 6 times larger than the HCF). And a 12x72 jigsaw has sidelengths with an LCM of 72 and a HCF of 12 which also does the trick. However, I'd suspect that the 36x24 would make a more standard jigsaw ratio.
5. Now back to the question. It's about the edges.
A 12x72 jigsaw has 12+12+72+72-4 edge pieces (don't forget those corner pieces shouldn;t be counted twice!)..That's 116 edges so 748 don't have straight edges..
A 36x24 jigsaw has 36+36+24+24-4 edge pieces..That's 164 edges so 700 don't have straight edges.
6. Incidentally, I should have figured this out before I completed your puzzle but there are two jigsaws such that the LCM is 24 times larger than the HCF, two that are 54, two that are 96, two that are 216 and two that are 864. "