Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of April. It begins, as usual with the puzzle of the month.
Cupcakes were being sold at three prices: large cupcakes were one pound each, medium cupcakes were two for a pound and small cupcakes were three for a pound. Some children (there were as many boys as girls and two of the girls were twins) were given seven pounds to spend on these cupcakes and each child received exactly the same types and number of cakes. How many cupcakes did each receive (no cupcakes were divided) ?
The answer and credit for this puzzle will be revealed next month but let me know if you figure it out before then.
It is so annoying when April Fools' Day does not fall on a school day. It robs the Maths teacher of the opportunity to catch their students with the One Out Of Ten lesson starter. This year I've added an old story lower down the page which shows how a paradox is used as an April Fools' Day joke.
Easter will be with us very soon and most of you will have already broken up for the Easter holidays. It's not too late however to spread the eggcitement of the season with your pupils by sending them an activity from The Easter Maths collection. I recommend Systematic Easter Eggs which has five levels of challenge.
Thanks to Sarah Carter @mathequalslove for the permission she gave for her puzzles to be used as challenges on the Factor Trees page. They really are fun to do and I've made it so that you can scribble on the diagram as you eliminate possibilities,
It has only just occured to me how closely related the topics of Parametric Equations and Composite Functions are. There is a Transum exercise for both concepts and I have now linked the former to the latter.
In response to a suggestion from Transum subscriber Sharon, there is now a new level 6 for the Compound Interest exercises. Sharon wrote "I wanted to give my Year 11s more practice of compound interest questions where an amount is also added regularly, ... I also think this is important as in real life situations we generally add amounts not just leave an amount in a savings account."
I have been slowly but surely adding topics to Advanced Refreshing Revision and am pleased to show you that there are quite a few to choose from now. This projectable resource is designed for students in Years 12 and 13 and I've already been using it with all of my older students.
I have just updated the Smallest Number activity page. If you have never done this with a class I suggest you do. The following three questions are probably harder to answer than those in the Advanced Refreshing Revision above. I would love to hear your thoughts on this:
I am grateful to Transum friend Ann who alerted me to breakthroughs in aperiodic tiling.
Mathematicians have recently discovered a 13-sided shape nicknamed "the hat", which is a significant breakthrough in geometry. It represents the first true example of an "einstein," a term derived from the German word for "one stone," that refers to a single shape capable of forming a unique tiling of a plane. For nearly half a century, mathematicians have been searching for such a shape. The tiles of "the hat" fit together seamlessly and can cover an infinite plane, but they are aperiodic, meaning they do not form a repeating pattern.
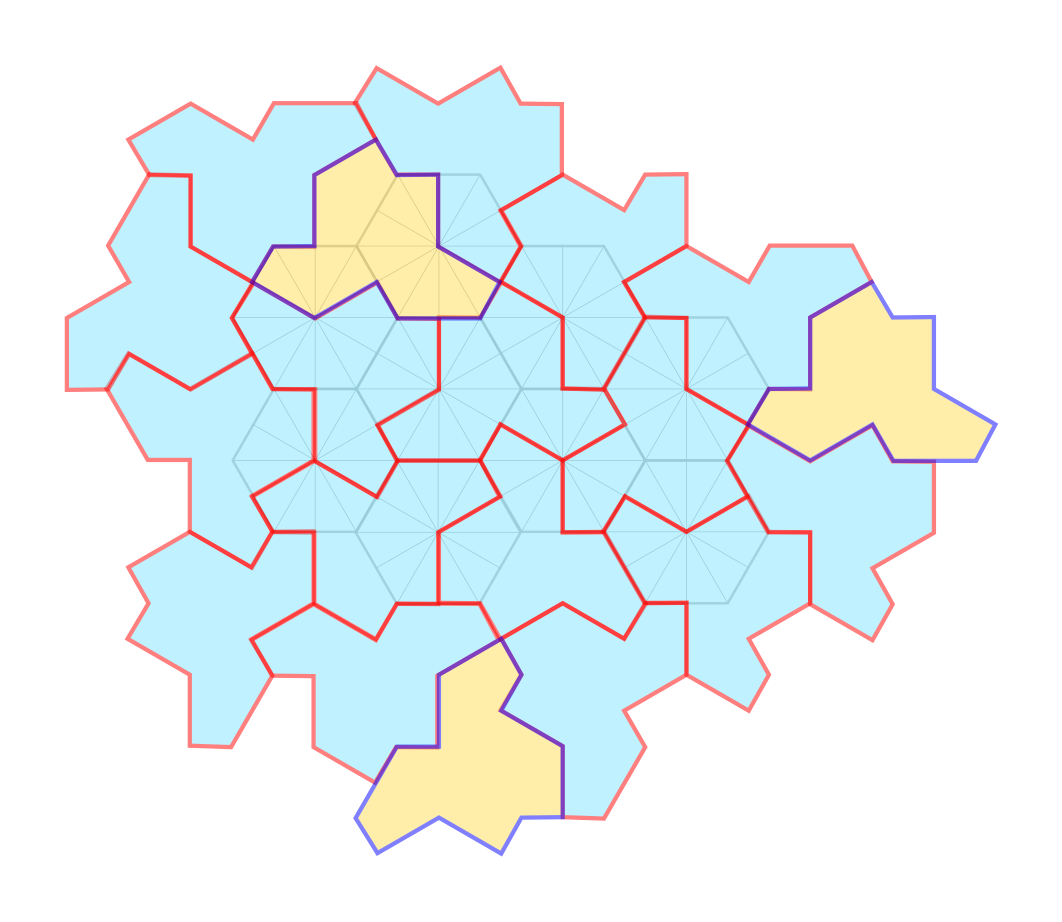
Gringer, CC BY-SA 4.0, via Wikimedia Commons
It all makes Tessellations look very pedestrian!
Finally the answer to last month's puzzle which was about making 100 from four sevens and a zero. My answer is 77 ÷ 0.77 making use of a decimal point and other answers were similar such as Martin's which was 7/7 x 7/.07
That's all for now,
John
P.S. I begin this month absolutely exhausted as I've just completed a 31 day March!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
