Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Before any of your students catch you out on April Fools’ Day be prepared to get your own back with the 1st April Starter of the Day. As well as being great fun (when you realise the joke) it also reminds the over-enthusiastic students to read instructions carefully.
This month’s puzzle is about a ship, travelling at constant speed away from the coast of Transumvania. A drone flies in the same direction as the ship at ten times its speed but doesn’t leave the coast until the ship is 180km away. How far does the drone travel until it reaches the ship? Answer next month – but do let me know if you solve it before then.
It has been a very busy month with many updates and additions made to the website. I have put countless hours into coding, filming, checking, designing and corresponding but it is all worthwhile when I see that every day thousands of trophies are being earned by students around the world. So here is a brief roundup of the upgrades and additions:
Tessellations has had a complete makeover. There are the ‘sandbox’ pages where students can practise putting shapes together without leaving any gaps. There are also two exercises and a Gallery. I have started taking pictures of tessellations in the real world to add to the gallery. Do you know the attributes that determine if a polygon tessellates?
Polygon Hunting is a challenge to find all the different polygons that can be drawn by joining dots in a certain nine-pin pattern. Each time you create a new polygon you can 'take a picture' of it in order to keep a record of your progress. This activity is based on an article Polygon Hunting: Extending the Field by W. A. Ewbank in a 1984 publication of the magazine Mathematics in School.
Vector Connectors is brand new (thanks to a suggestion from a subscriber) and works well with the existing Vectors activity (which has been updated and extended). There are two new help videos with those activities too. Finally I have just put the finishing touches to Vectors – Magnitude and Direction. I guess that’s what they call a trilogy!
The old activity, Using Graphs to Solve Equations, now has 3 new levels. Not many trophies have been claimed for the new levels yet. They must be too niche!
To prevent you from going round in circles here is a pair of compasses!
Whether it be Songkran or Easter I think most Transum users around the world have a holiday from school at this time of year. I invite you and your students to enjoy the collection of Easter activities which include plenty of End of Term and Holiday Activities which are not to be missed.
The very first real trophy has been awarded to the first person to collect 1000 Transum virtual trophies. What a fantastic achievement.
Finally the answer to last month's puzzle which was “A right-handed dice is placed on the near-left square of a chess board with the number one face uppermost and the number two face facing left. The edges of the dice are the same length as the sides of the chess board squares. The dice is alternately rolled one square forward then one square to the right until it reaches the far-right square. What number face is on top of the dice now?”
The answer is 2
A couple of people chose to think of the unfolded nets of the dice being laid across the chessboard to show which numbers were either on the bottom or on the top of the dice at each square. It can then be seen that the numbers on the leading diagonal were a repeating sequence of powers of two.
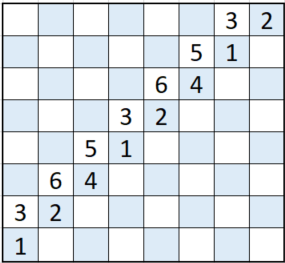
Furthermore I extended the solution to an n by n grid of squares to be \( 2^{(n-1) \, \text{mod} \, 3} \) where \(x \, \text{mod} \, y\) means the remainder when x is divided by y.
That’s all for now.
Stay safe, take care and seize the day!
John
P.S. If you are asked to subtract five squared from the square root of six hundred and twenty five, say nothing and you'll be correct!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
