Transum Software

Trapezium Rule

Practise using the trapezium rule to find an approximate value for the area under a curve.
Menu Level 1 Level 2 Level 3 Exam-Style Help Calculus

Answers with more than three significant figures should be rounded to three significant figures.

Use the trapezium rule with six intervals to find an approximation of the area above the x axis and under the graph of \(y = 4x - x^2 \) between \(x=1\) and \(x = 4\).

 Correct Wrong

Find an approximation of the area between the x axis and the graph of \(y = \cos(x) + 2 \) between 30° and 50° using the trapezium rule with four trapeziums.
Graph

 Correct Wrong

Use the trapezium rule with five ordinates to find an approximation of
$$ \int^{5}_1 (x-3)^2 \; \text{dx} $$

 Correct Wrong

Use the trapezium rule with four intervals to find an approximation of
$$ \int^{2}_{-2} \frac{1}{x^2+1} \; \text{dx} $$

 Correct Wrong

Use the trapezium rule with five ordinates to find an approximation of the area above the x axis and under the graph of \(y = \sqrt{1+x^2} \) for \( 1 \le x \le 3\).

 Correct Wrong

 

Check

This is Trapezium Rule level 2. You can also try:
Level 1 Level 3

Instructions

Try your best to answer the questions above. Type your answers into the boxes provided leaving no spaces. As you work through the exercise regularly click the "check" button. If you have any wrong answers, do your best to do corrections but if there is anything you don't understand, please ask your teacher for help.

When you have got all of the questions correct you may want to print out this page and paste it into your exercise book. If you keep your work in an ePortfolio you could take a screen shot of your answers and paste that into your Maths file.
Why am I learning this?

Mathematicians are not the people who find Maths easy; they are the people who enjoy how mystifying, puzzling and hard it is. Are you a mathematician?

Comment recorded on the 5 April 'Starter of the Day' page by Mr Stoner, St George's College of Technology:

"This resource has made a great deal of difference to the standard of starters for all of our lessons. Thank you for being so creative and imaginative."

Comment recorded on the 10 April 'Starter of the Day' page by Mike Sendrove, Salt Grammar School, UK.:

"A really useful set of resources - thanks. Is the collection available on CD? Are solutions available?"

Each month a newsletter is published containing details of the new additions to the Transum website and a new puzzle of the month.

The newsletter is then duplicated as a podcast which is available on the major delivery networks. You can listen to the podcast while you are commuting, exercising or relaxing.

Transum breaking news is available on Twitter @Transum and if that's not enough there is also a Transum Facebook page.
Featured Activity

Numskull

Numskull

Interactive, randomly-generated, number-based logic puzzle based on the Latin square designed to develop numeracy skills. These puzzles are drag and drop and can earn you a Transum Trophy.

Answers

There are answers to this exercise but they are available in this space to teachers, tutors and parents who have logged in to their Transum subscription on this computer.

A Transum subscription unlocks the answers to the online exercises, quizzes and puzzles. It also provides the teacher with access to quality external links on each of the Transum Topic pages and the facility to add to the collection themselves.

Subscribers can manage class lists, lesson plans and assessment data in the Class Admin application and have access to reports of the Transum Trophies earned by class members.

If you would like to enjoy ad-free access to the thousands of Transum resources, receive our monthly newsletter, unlock the printable worksheets and see our Maths Lesson Finishers then sign up for a subscription now:

Subscribe

Go Maths

Learning and understanding Mathematics, at every level, requires learner engagement. Mathematics is not a spectator sport. Sometimes traditional teaching fails to actively involve students. One way to address the problem is through the use of interactive activities and this web site provides many of those. The Go Maths page is an alphabetical list of free activities designed for students in Secondary/High school.

Maths Map

Are you looking for something specific? An exercise to supplement the topic you are studying at school at the moment perhaps. Navigate using our Maths Map to find exercises, puzzles and Maths lesson starters grouped by topic.

Teachers

If you found this activity useful don't forget to record it in your scheme of work or learning management system. The short URL, ready to be copied and pasted, is as follows:

Alternatively, if you use Google Classroom, all you have to do is click on the green icon below in order to add this activity to one of your classes.

It may be worth remembering that if Transum.org should go offline for whatever reason, there is a mirror site at Transum.info that contains most of the resources that are available here on Transum.org.

When planning to use technology in your lesson always have a plan B!

Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Apple

For Students:

 

Transum.org is a proud supporter of the kidSAFE Seal Program

For Teachers:

For All:

©1997-2024 WWW.TRANSUM.ORG

© Transum Mathematics 1997-2024
Scan the QR code below to visit the online version of this activity.

This is a QR Code

https://www.Transum.org/go/?Num=885

Description of Levels

Close

Close

Level 1 - A structured single question with many parts

Level 2 - Five practice questions

Level 3 - Questions requiring a little more thought

Exam-Style - Have a go at an IB/A-level exam-style questions (worked solutions are available for Transum subscribers).

Calculus a collection of lesson Starters, visual aids, investigations and self-marking exercises.

Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.

Log in Sign up

Example

The video above comes from Revision Village

Sometimes the area under a curve cannot be found by integration. In these cases a method to approximate the area under the curve called the trapezium rule can be used.

The rule divides the area under a curve into trapeziums, calculates their areas, then sums these areas to get an approsimation of the total area.

Area of a trapezium

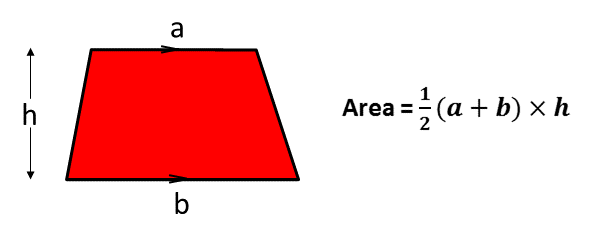
Formula for the area of a trapezium

Trapezium Rule

If the width of each interval is \(h\) and the y values (ordinates) are denoted as \(y_0, y_1, y_2, y_3 ...\) then the formula for finding the sum of the areas of these trapeziums is

$$ \frac12 h ((y_0 + y_n) + 2(y_1 + y_2 + ... + y_{n-1})) $$

where n is the number of intervals.

Note that the number or ordinates is always one more than the number of intervals.

If the lower bound of the required area is \(p\) and the upper bound is \(q\) then

$$ h= \frac{q-p}{n} $$

The more trapeziums the area is divided into the more accurate the estimate.

When the gradient of the graph is increasing over the given interval the area given by the trapezium rule will be an overestimate of the actual area.

When the gradient of the graph is decreasing over the given interval the area given by the trapezium rule will be an underestimate of the actual area.

Don't wait until you have finished the exercise before you click on the 'Check' button. Click it often as you work through the questions to see if you are answering them correctly. You can double-click the 'Check' button to make it float at the bottom of your screen.

Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.

Log in Sign up

Close

Close