Amortisation and Annuities

Instructions Try your best to answer the questions above. Type your answers into the boxes provided leaving no spaces. As you work through the exercise regularly click the "check" button. If you have any wrong answers, do your best to do corrections but if there is anything you don't understand, please ask your teacher for help. When you have got all of the questions correct you may want to print out this page and paste it into your exercise book. If you keep your work in an ePortfolio you could take a screen shot of your answers and paste that into your Maths file.

	You are learning this because future ideas are built on previous ideas and the more ideas you learn the more power you have to learn anything, ever! The world's best football player engages in rigorous training, practicing skills repeatedly to prepare for the big game. While the specific actions rehearsed during these exercises are rarely needed in the match, the very process of performing these drills enhances their overall prowess as a top player. more...	More Activities: Maths Map Go Maths Games Puzzles Times Tables TablesMaster iPad Maths Investigations Exam Questions
Mathematicians are not the people who find Maths easy; they are the people who enjoy how mystifying, puzzling and hard it is. Are you a mathematician? Comment recorded on the 3 October 'Starter of the Day' page by Mrs Johnstone, 7Je: "I think this is a brilliant website as all the students enjoy doing the puzzles and it is a brilliant way to start a lesson." Comment recorded on the 1 February 'Starter of the Day' page by M Chant, Chase Lane School Harwich: "My year five children look forward to their daily challenge and enjoy the problems as much as I do. A great resource - thanks a million."		Each month a newsletter is published containing details of the new additions to the Transum website and a new puzzle of the month. The newsletter is then duplicated as a podcast which is available on the major delivery networks. You can listen to the podcast while you are commuting, exercising or relaxing. Transum breaking news is available on Twitter @Transum and if that's not enough there is also a Transum Facebook page.
Featured Activity Shunting Puzzles These puzzles are Transum's versions of the shunting or switching puzzles made popular by train enthusiasts and logic puzzle solvers.	Answers There are answers to this exercise but they are available in this space to teachers, tutors and parents who have logged in to their Transum subscription on this computer. A Transum subscription unlocks the answers to the online exercises, quizzes and puzzles. It also provides the teacher with access to quality external links on each of the Transum Topic pages and the facility to add to the collection themselves. Subscribers can manage class lists, lesson plans and assessment data in the Class Admin application and have access to reports of the Transum Trophies earned by class members. If you would like to enjoy ad-free access to the thousands of Transum resources, receive our monthly newsletter, unlock the printable worksheets and see our Maths Lesson Finishers then sign up for a subscription now: Subscribe
Go Maths Learning and understanding Mathematics, at every level, requires learner engagement. Mathematics is not a spectator sport. Sometimes traditional teaching fails to actively involve students. One way to address the problem is through the use of interactive activities and this web site provides many of those. The Go Maths page is an alphabetical list of free activities designed for students in Secondary/High school. Maths Map Are you looking for something specific? An exercise to supplement the topic you are studying at school at the moment perhaps. Navigate using our Maths Map to find exercises, puzzles and Maths lesson starters grouped by topic.
Teachers
If you found this activity useful don't forget to record it in your scheme of work or learning management system. The short URL, ready to be copied and pasted, is as follows:	Alternatively, if you use Google Classroom, all you have to do is click on the green icon below in order to add this activity to one of your classes.	It may be worth remembering that if Transum.org should go offline for whatever reason, there is a mirror site at Transum.info that contains most of the resources that are available here on Transum.org. When planning to use technology in your lesson always have a plan B!
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.

For Students:

For Teachers:

For All:

Transum.org is a proud supporter of the kidSAFE Seal Program

Help

These exercises are designed for those who have access to a graphic display calculator (GDC) with a Finance Solver function. It is possible to answer the questions using only a scientific calculator but not easy.

A great way to answer the questions in these exercises without a GDC is by creating a table of interest, payment and balance in a spreeadsheet.

Amortisation

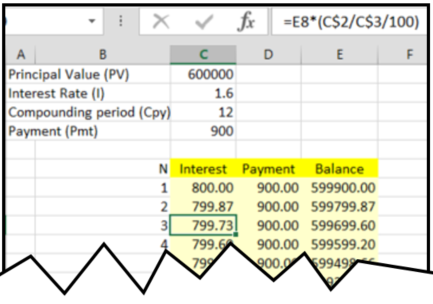
Amortization is is paying off an amount owed over time by making planned, incremental payments of principal and interest. In accounting, amortisation refers to writing off an asset's cost as an expense over its estimated useful life to reduce a company's taxable income.

The word amortise (which can also be spelled amortize) comes from the latin ad mortem meaning 'to death'

The formula to find the payments for amortisation is:

$$ Pmt = PV \times \frac{r(1+r)^n}{(1+r)^n -1} $$

$Pmt$ is the amount of each regular payment being made to pay off the loan.
$PV$ is the present value or the initial amount of the loan.
$r$ is the nominal APR divided by the number of payments per year expressed as a decimal (unlike I used in the Solver function below)
$n$ is the total number of payments that will be made to pay off the loan.

It is recommended to use the Finance Solve on your GDC for this topic. [See TI-Nspire Essentials].

menu ⇒ Finance ⇒ Finance Solver

These are the variables used in the Finance Solver function:

$N$ is the total number of payments that will be made to pay off the loan.
$I$ is the rate of compound interest.
$PV$ is the present value (a positive number) or the initial amount of the loan.
$Pmt$ is the amount of each regular payment being made to pay off the loan (a negative value).
$FV$ is the future value. It the loan is to be paid off in full this will be zero.
$PpY$ is the number of payments per year.
$CpY$ is the number of interest calculation periods per year; E.g. this would be 12 if compounded monthly.
$PmtAt$ is usually set to END as this is when the load is completely paid off.
[Note that N ÷ PpY gives the number of years it will take to pay off the loan]

There is also a function on the GDC that can produce a table showing all the datails of the gradual loan repayment:

menu ⇒ Finance ⇒ Amortisation ⇒ Amortisation Table

These are the variables used in the Amortisation Table function:

$NPmt$ is the number of rows you would like the calculator to show as sometimes showing all rows would clutter the calculator screen.
$N$ is the total number of payments that will be made to pay off the loan.
$I$ is the rate of compound interest.
$PV$ is the present value (a positive number) or the initial amount of the loan.
$Pmt$ is the amount of each regular payment being made to pay off the loan.
$FV$ is the future value. It the loan is to be paid off in full this will be zero.
$PpY$ is the number of payments per year.
$CpY$ is the number of interest calculation periods per year; E.g. this would be 12 if compounded monthly.

The values should be typed into the function in this order:

amortTbl(NPmt,N,I,PV,Pmt,FV,PpY,CpY)

Column 1 is the number of the repayment
Column 2 is the amount of interest paid off at that time.
Column 3 is the amount of principal paid off at that time.
Column 4 is the balance of the loan at the end of at that time period.

Annuity

An annuity is the investment of a lump-sum which provides the fund from which regular withdrawals are made over a fixed time period. The investment earns interest according to the balance of the annuity each time period. The payments may be made weekly, monthly, quarterly, yearly, or at any other regular interval of time.

An annuity which provides for payments for the remainder of a person's lifetime is a life annuity.

It is recommended to use a GDC for your working. See TI-Nspire Essentials for an example of how to use the Finance Solver. Note that PV (present value, the amount of the lump-sum) should be negative and the payments (PMT) should be positive.

The formula for calculating the payments from an annuity is the same as that for an amortisation

Don't wait until you have finished the exercise before you click on the 'Check' button. Click it often as you work through the questions to see if you are answering them correctly. You can double-click the 'Check' button to make it float at the bottom of your screen.

Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.

Megan retired at the age of 64. She invested £700000 in an annuity fund which returns 6% p.a. compounded monthly. She wants the money to last for 30 years. 1. Calculate how much she can afford to withdraw each month.	£
Megan's sister retired at the age of 55. She invested £700000 in an annuity fund which returns 3.8% p.a. compounded monthly. She withdraws £3500 each month for living expenses and holidays. 2. Calculate how long it will take for the money to run out. Round you answer down to a whole number of years.
Megan's brother deposits $630000 in an annuity fund which earns 3.3% p.a. interest compounded quarterly. He wants the money to last for 20 years. 3. How much can he afford to withdraw each quarter?	$
4. Find the outstanding balance of Megan's brother's fund after 10 years.	$
Professor Collins invested £700000 in an annuity fund which returns 2.4% p.a. compounded monthly. He withdraws £3000 each month. 5. Calculate how long it will take for the money to run out. Round you answer down to a whole number of years.
6. How many more months would his money last if he only withdrew £2500 each month? Round you answer down to a whole number of months.
7. If £40000 is invested with a 1.2% p.a. interest rate (compounded annually). What is the maximum I can take out of this account at the end of each year if it is to be a perpetuity (a special type of annuity in which the regular payments continue indefinitely)?	£
8. What amount must be initially invested into an annuity account if it is to yield £2000 per month for 20 years at a 2% p.a. rate of interest componded monthly?	£
Dr Jane Dose retires at age 63 with €75000 in her savings fund. She rolls this money into an annuity fund earning 3.5% p.a. interest compounded monthly. 9. How much will she be able to withdraw each month if her money is to last until her 85th birthday?	€
10. How much more will Dr Dose be able to withdraw each month if her money was to only last one decade?	€

Amortisation and Annuities

Exercises containing problems about gradually paying off loans and calculating pension plans.

Interest Amortisation Annuities Exam-Style Description Help More Finance

Instructions

More Activities:

Featured Activity

Shunting Puzzles

Answers

Go Maths

Maths Map

Teachers

Description of Levels