
 |
Miscellaneous Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. The questions shown here or their solutions contain the text 'Cumulative'. |
1. | GCSE Higher [310] |
This Cumulative Frequency graph shows the heights of 58 Scouts. Work out an estimate for the number of these Scouts with a height greater than 160cm.
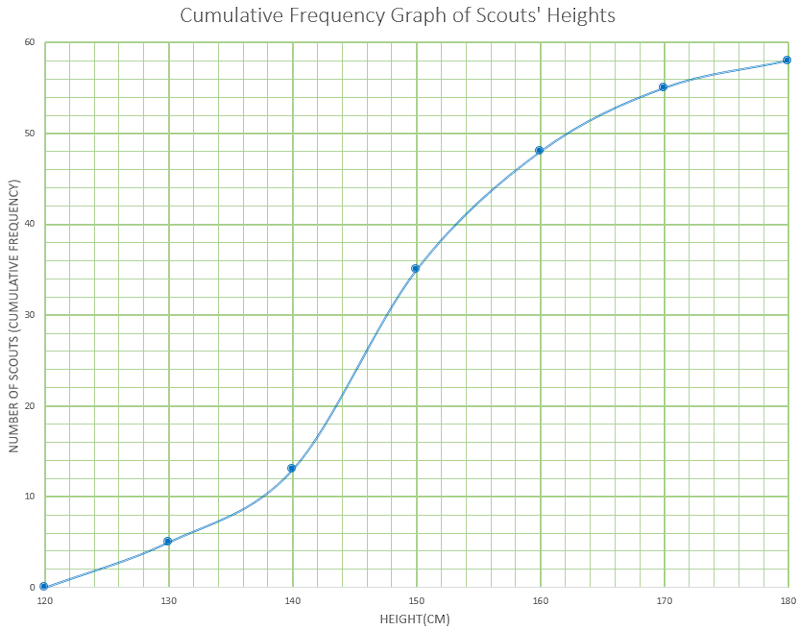
2. | GCSE Higher [519] |
The grouped frequency table gives information about the times, in minutes, that 90 commuters take to get home from work.
| Time (t minutes) | Frequency |
|---|---|
| \(0 \lt t \le 10\) | 6 |
| \(10 \lt t \le 20\) | 32 |
| \(20 \lt t \le 30\) | 22 |
| \(30 \lt t \le 40\) | 10 |
| \(40 \lt t \le 50\) | 10 |
| \(50 \lt t \le 60\) | 7 |
| \(60 \lt t \le 70\) | 3 |
(a) Complete the cumulative frequency table.
| Time (t minutes) | Cumulative frequency |
|---|---|
| \(0 \lt t \le 10\) | |
| \(0 \lt t \le 20\) | |
| \(0 \lt t \le 30\) | |
| \(0 \lt t \le 40\) | |
| \(0 \lt t \le 50\) | |
| \(0 \lt t \le 60\) | |
| \(0 \lt t \le 70\) |
(b) On the grid, draw the cumulative frequency graph for this information.
(c) Use your graph to find an estimate for the percentage of these commuters who take more than 45 minutes to get home from work.
3. | GCSE Higher [701] |
The distance walked by each of 68 hikers was recorded. The results are shown in the cumulative frequency curve.
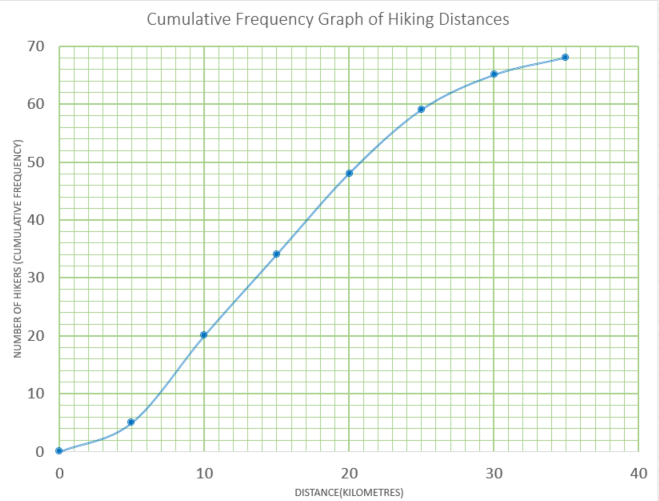
(a) Estimate the median.
(b) Estimate the interquartile range.
(c) Use the curve to complete the frequency table.
| Distance(\(d\) km) | 0 < d ≤ 5 | 5 < d ≤10 | 10 < d ≤ 15 | 15 < d ≤ 20 | 20 < d ≤ 25 | 25 < d ≤ 30 | 30 < d ≤ 35 |
|---|---|---|---|---|---|---|---|
| Frequency | 5 | 15 |
(d) Write down the modal class.
(e) Calculate an estimate for the mean.
4. | GCSE Higher [153] |
The table shows the marks earned by 200 students taking a Maths exam.
| Mark (n) | \(0\lt n \le 10\) | \(10\lt n \le 20\) | \(20\lt n \le 30\) | \(30\lt n \le 40\) | \(40\lt n \le 50\) | \(50\lt n \le 60\) | \(60\lt n \le 70\) | \(70\lt n \le 80\) |
| Frequency | 3 | 7 | 33 | 42 | 54 | 35 | 20 | 6 |
(a) Use the data in the table above to complete the following cumulative frequency table
| Mark (n) | \(n \le 10\) | \(n \le 20\) | \(n \le 30\) | \(n \le 40\) | \(n \le 50\) | \(n \le 60\) | \(n \le 70\) | \(n \le 80\) |
| Cumulative Frequency | 200 |
(b) Draw the cumulative frequency curve on graph paper.
The top 5% of students will receive an A grade. The next 15% of students will receive a B grade and the next 30% will receive a C grade.
(c) Use your graph to estimate the lowest mark that B grade will be awarded for.
5. | IB Studies [108] |
The following grouped frequency table shows the length of time, \(t\), in minutes, visitors watched an octopus swimming around a tank at an aquarium.
| Time (\(t\)) | Visitors |
|---|---|
| \(0\lt t \le 5\) | 23 |
| \(5\lt t \le 10\) | 13 |
| \(10\lt t \le 15\) | 9 |
| \(15\lt t \le 20\) | 6 |
| \(20\lt t \le 25\) | 2 |
| \(25\lt t \le 30\) | 1 |
(a) Write down the total number of visitors who were included in the survey.
(b) Write down the mid-interval value for the \(20\lt t \le 25\) group.
(c) Find an estimate of the mean time visitors took watching the octopus.
The information above has been rewritten as a cumulative frequency table.
| Time (\(t\)) | \(t \le 5\) | \(t \le 10\) | \(t \le 15\) | \(t \le 20\) | \(t \le 25\) | \(t \le 30\) |
|---|---|---|---|---|---|---|
| Cumulative frequency | 23 | 36 | \(a\) | 51 | 53 | \(b\) |
(d) Write down the values of \(a\) and \(b\).
This information is shown in the following cumulative frequency graph.
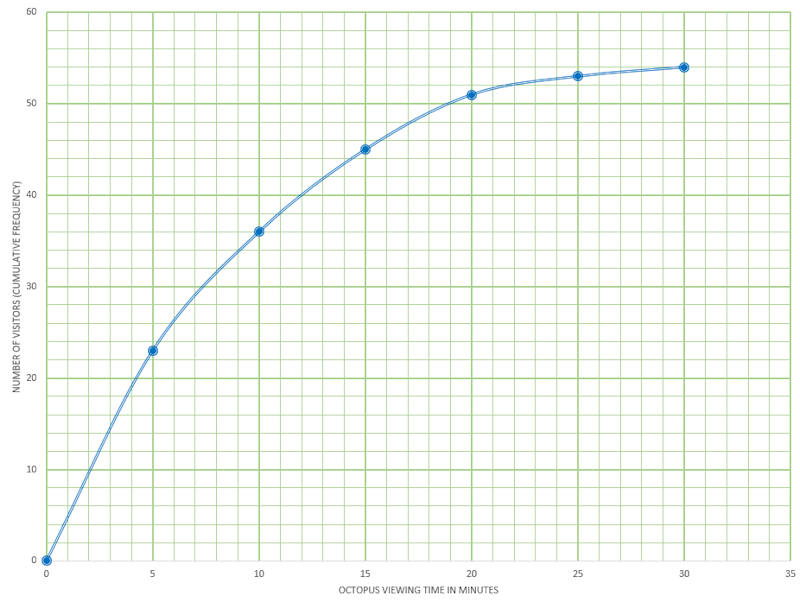
(e) Use the graph to estimate the maximum time taken watching the octopus for the first 32 visitors (arranged in order of increasing viewing time).
(f) Use the graph to estimate the number of visitors who spent less than 13 minutes watching the octopus.
(g) Use the graph to estimate the number of visitors who take more than 17 minutes watching the octopus.
6. | GCSE Higher [219] |
The table shows the test marks for 31 students.
| Percentage (p) | Frequency |
| 5 ≤ p < 15 | 2 |
| 15 ≤ p < 25 | 3 |
| 25 ≤ p < 35 | 4 |
| 35 ≤ p < 45 | 3 |
| 45 ≤ p < 55 | 8 |
| 55 ≤ p < 65 | 8 |
| 65 ≤ p < 75 | 2 |
| 75 ≤ p < 85 | 1 |
Marco drew this cumulative frequency graph using the data.
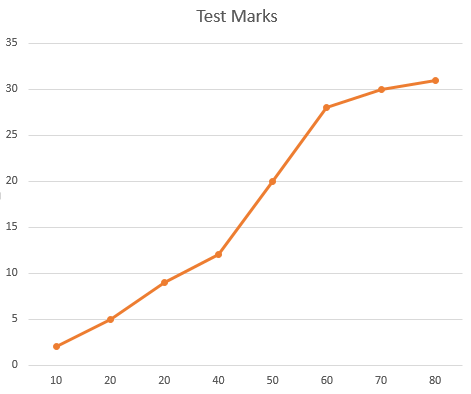
Make three criticisms of Marco’s graph.
7. | IB Standard [29] |
The following table shows the number of days families spend in a particular seaside hotel in August last year.
| Days | Frequency | Cumulative frequency |
|---|---|---|
| 2 | 3 | 3 |
| 5 | 11 | 14 |
| 7 | 15 | 29 |
| 10 | \(x\) | 39 |
| 14 | 5 | 44 |
(a) Find the value of \(x\).
(b) Find the mean.
(c) Find the variance.
8. | IB Analysis and Approaches [663] |
A programmer recorded the number of web pages she had created since she had begun working for the Corney Content Creation Company. The following table shows the number of days, \(d\), and the cumulative total number of web pages, \(p\).
| Number of days \((d)\) | 5 | 9 | 16 | 18 | 23 | 29 | 32 | 40 | 50 |
| Number of pages \((p)\) | 14 | 28 | 47 | 54 | 65 | 90 | 95 | 123 | 156 |
The value of Pearson's product moment correlation coefficient, \(r\) for this data is 0.999 to three significant figures.
(a) The regression line of \(p\) on \(d\) for this data can be written in the form \(p=ad + b\). Find the value of a and the value of b.
(b) Use your regression line to estimate the number of web pages created by day 45.

9. | IB Analysis and Approaches [667] |
The heights, H metres, of flowers called Xylothorn Blooms growing in the dense forests of Verdantem on the luminous planet Aurorion can be modelled by a normal distribution with mean 14.3 metres and standard deviation 3.9 metres.

(a) One of the flowers is selected at random. Find the probability that its height more than 15.5 metres.
According to this model, 40% of the flowers have a height between \(x\) metres and 15.5 metres.
(b) Find the probability that a randomly selected flower has a height less than \(x\) metres.
(c) Find the value of \(x\).
(d) Ten flowers are selected at random.
Find the probability that no more than two of the flowers has a height less than \(x\) metres.
10. | IB Analysis and Approaches [759] |
In Avianville, the probability that a bird will leave a mess on my car on any given day is independent of whether a mess was left on any other day. During July, the probability of a mess being left is \(0.15\). July has 31 days.
Find the probability that
(a) a mess was left on exactly 5 days in July;
(b) a mess was left on at least 5 days in July;
(c) the first day that a mess was left in July is on the 8th day.

11. | IB Standard [60] |
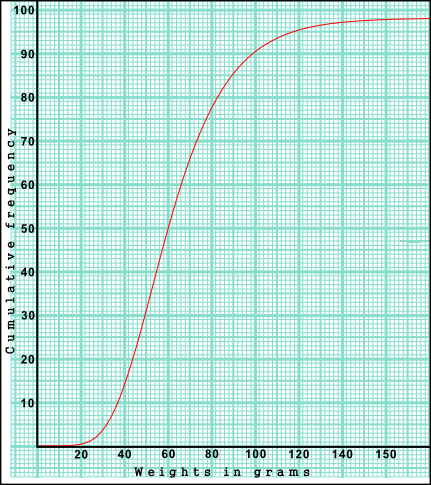
The weights in grams of 98 mice are shown in the cumulative frequency diagram. The heaviest mouse weighted 160g.
(a) Write down the median weight of the mice.
(b) Find the percentage of mice that weigh 70 grams or less.
The same data is presented in the following table.
| Weights w grams | 0 < w ≤ 40 | 40 < w ≤ 80 | 80 < w ≤ 120 | 120 < w ≤ 160 |
|---|---|---|---|---|
| Frequency | p | 63 | q | 3 |
(c) Find the value of p.
(d) Find the value of q.
(e) Use the values from the table to estimate the mean and standard deviation of the weights.
A second batch of mice are normally distributed with the same mean and standard deviation as those of the first group mentioned above.
(f) Find the percentage of the second batch of mice that weigh 70 grams or less.
(g) A sample of five mice is chosen at random from the second batch. Find the probability that at most three mice weigh 70 grams or less.
12. | IB Analysis and Approaches [413] |
A TV company surveyed 88 of its employees to find out how much time they spend travelling to work on a given day. The results of the survey are shown in the following cumulative frequency diagram.
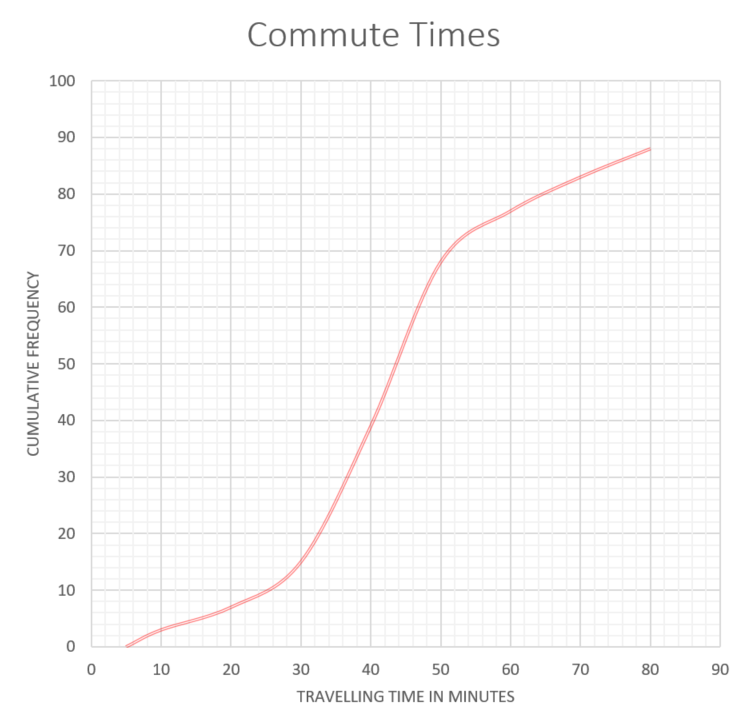
(a) Find the median number of minutes spent travelling to work.
(b) Find the interquartile range.
(c) Find the number of employees whose travelling time is within 20 minutes of the median.
(d) Only 10% of the employees spent less than k minutes travelling to work. Find the value of k.
The results of the survey can also be displayed on the following box-and-whisker diagram.
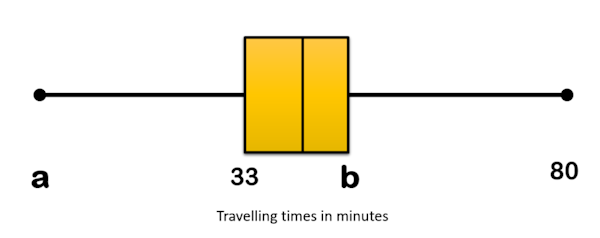
(e) Write down the value of a.
(f) Find the value of b.
(g) Travelling times of less than p minutes are considered outliers. Find the value of p .
13. | IB Studies [206] |
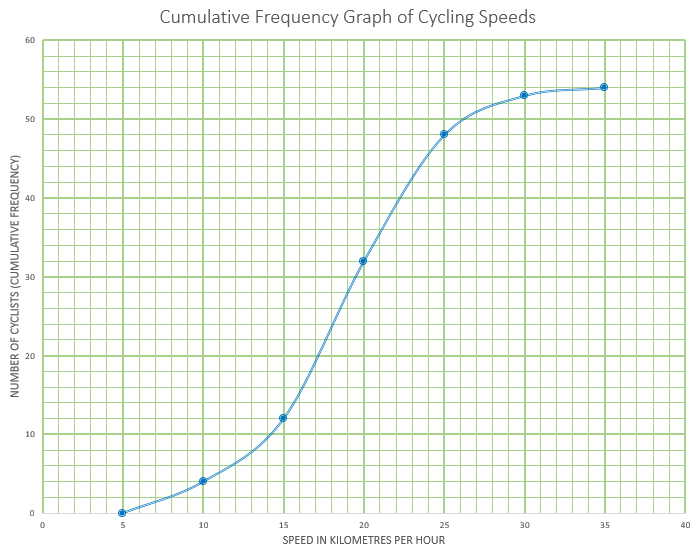
This cumulative frequency graph shows the speeds in kmh-1 of cyclists passing a certain point on a race track.
(a) Estimate the minimum possible speed of one of these cyclists.
(b) Find the median speed of the cyclists.
(c) Write down the 65th percentile.
(d) Calculate the interquartile range.
(e) Find the number of these cyclists that were travelling faster than 22 kmh-1
The table shows the speeds of these cyclists.
| Speed of Cyclists (s) | Number of Cyclists |
|---|---|
| \(0 \lt s \le 5\) | 0 |
| \(5 \lt s \le 10\) | \(a\) |
| \(10 \lt s \le 15\) | 8 |
| \(15 \lt s \le 20\) | 20 |
| \(20 \lt s \le 25\) | 16 |
| \(25 \lt s \le 30\) | 5 |
| \(30 \lt s \le 35\) | \(b\) |
(f) Find the value of \(a\) and of \(b\)
(g) Write down the modal class.
(h) Write down the mid-interval value for the modal class.
(i) Use your graphic display calculator to calculate an estimate of the mean speed of these cyclists.
(j) Use your graphic display calculator to calculate an estimate of the standard deviation of the speeds of these cyclists.
14. | IB Analysis and Approaches [581] |
Gringe Hull Secondary School has students from Year 7 to Year 13. A group of 138 students in Year 9 were randomly selected and surveyed to find out how long it takes them to travel to school each morning. Their results are represented by the following cumulative frequency graph.
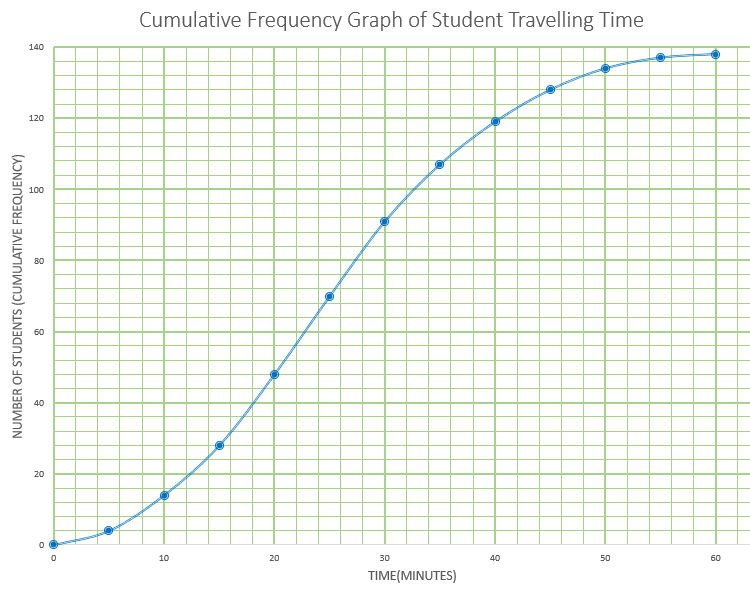
(a) Find the median number of minutes per day these Year 9 students spend travelling to school.
(b) Given that 20% of these Year 9 students spend more than \(k\) minutes per day travelling to school, find value of \(k\).
The same information is represented by the following table.
| Travelling time (m) in minutes | Frequency |
|---|---|
| 0 < m ≤ 5 | 4 |
| 5 < m ≤ 10 | 10 |
| 10 < m ≤ 15 | 14 |
| 15 < m ≤ 20 | \(p\) |
| 20 < m ≤ 25 | 22 |
| 25 < m ≤ 30 | 21 |
| 30 < m ≤ 35 | 16 |
| 35 < m ≤ 40 | \(q\) |
| 40 < m ≤ 45 | 9 |
| 45 < m ≤ 50 | 6 |
| 50 < m ≤ 55 | 3 |
| 55 < m ≤ 60 | 1 |
(c) Find the value of \(p\) and the value of \(q\).
There are 450 students in Year 9 at this school.
(d) Estimate the number of Year 9 students that spend less than 15 minutes travelling to school each day.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.