|
|
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | IB Standard |
The personal trainer collected data from a randomly selected sample of days. From this he found that the number glasses of water he drank in a day had a mean of 4.35.
| Glasses | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Frequency | 3 | 5 | 5 | 8 | \(x\) | 7 | 6 |
(a) Find the number of days represented by \(x\)
(b) Write down the standard deviation.
2. | IB Standard |
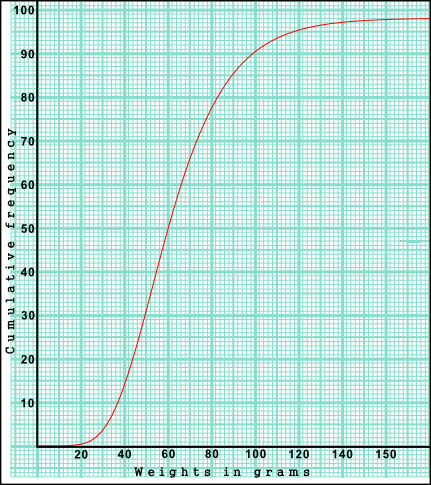
The weights in grams of 98 mice are shown in the cumulative frequency diagram. The heaviest mouse weighted 160g.
(a) Write down the median weight of the mice.
(b) Find the percentage of mice that weigh 70 grams or less.
The same data is presented in the following table.
| Weights w grams | 0 < w ≤ 40 | 40 < w ≤ 80 | 80 < w ≤ 120 | 120 < w ≤ 160 |
|---|---|---|---|---|
| Frequency | p | 63 | q | 3 |
(c) Find the value of p.
(d) Find the value of q.
(e) Use the values from the table to estimate the mean and standard deviation of the weights.
A second batch of mice are normally distributed with the same mean and standard deviation as those of the first group mentioned above.
(f) Find the percentage of the second batch of mice that weigh 70 grams or less.
(g) A sample of five mice is chosen at random from the second batch. Find the probability that at most three mice weigh 70 grams or less.
3. | IB Studies |
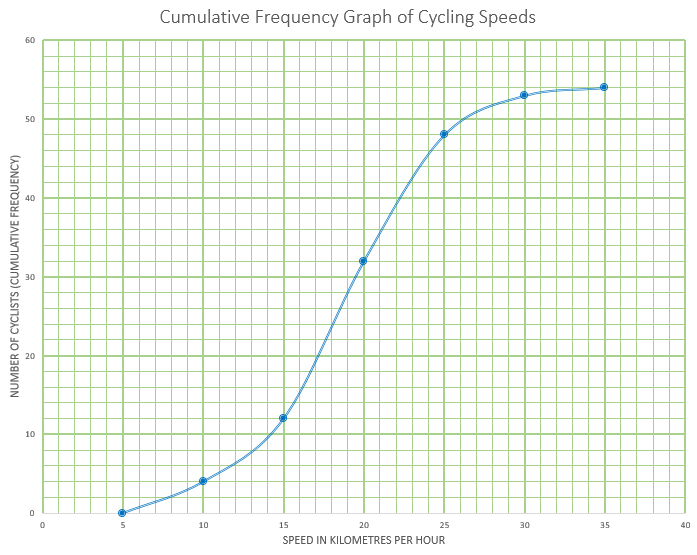
This cumulative frequency graph shows the speeds in kmh-1 of cyclists passing a certain point on a race track.
(a) Estimate the minimum possible speed of one of these cyclists.
(b) Find the median speed of the cyclists.
(c) Write down the 65th percentile.
(d) Calculate the interquartile range.
(e) Find the number of these cyclists that were travelling faster than 22 kmh-1
The table shows the speeds of these cyclists.
| Speed of Cyclists (s) | Number of Cyclists |
|---|---|
| \(0 \lt s \le 5\) | 0 |
| \(5 \lt s \le 10\) | \(a\) |
| \(10 \lt s \le 15\) | 8 |
| \(15 \lt s \le 20\) | 20 |
| \(20 \lt s \le 25\) | 16 |
| \(25 \lt s \le 30\) | 5 |
| \(30 \lt s \le 35\) | \(b\) |
(f) Find the value of \(a\) and of \(b\)
(g) Write down the modal class.
(h) Write down the mid-interval value for the modal class.
(i) Use your graphic display calculator to calculate an estimate of the mean speed of these cyclists.
(j) Use your graphic display calculator to calculate an estimate of the standard deviation of the speeds of these cyclists.
4. | IB Studies |
The table below shows the scores for 12 students on two Mathematic exam papers. For the first paper calculators were allowed and for the second paper they were not.
| Paper 1 (\(x\)) | 74 | 73 | 65 | 75 | 68 | 72 | 69 | 71 | 83 | 68 | 68 | 73 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Paper 2 (\(y\)) | 75 | 83 | 69 | 77 | 71 | 77 | 68 | 76 | 84 | 69 | 71 | 75 |
(a) Write down the mean score on Paper 1.
(b) Write down the standard deviation of the scores for Paper 1.
(c) Find the number of students that had a score of more than one standard deviation below the mean on Paper 1.
(d) Write down the correlation coefficient, \(r\).
(e) Write down the equation of the regression line of \(y\) on \(x\).
Another student scored 75 on Paper 1.
(f) Calculate an estimate of his score on Paper 2
Another student scored 88 on Paper 1.
(g) Determine whether you can use the equation of the regression line to estimate his score on Paper 2. Give a reason for your answer.
5. | IB Standard |
A data set has \(n\) items. The sum of the items is 650, the mean is 13 and the standard deviation is 5.
(a) Find n.
If each value in the set is multiplied by 7:
(b) Write down the value of the new mean;
(c) Find the value of the new variance.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
