Investigations Starters:

Work out the number of stamps needed to post a parcel.

How many different ways can four people stand in line?

Questions about the Small LEDs used to make up the digits on a calculator display.
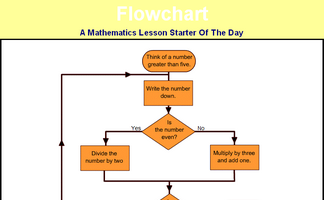
Use the flowchart to generate a sequence of numbers. Which number will reach 1 the fastest?
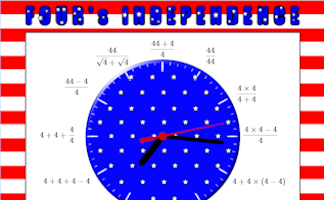
A clock face containing only the number 4. Can you make a clock face containing any other single number?

If all the students in this room shook hands with each other, how many handshakes would there be altogether?

To find out whether a number is happy or not, square each of its digits, add the answers and repeat. If you end up with 1 the number is happy! How many other happy numbers can you find?

A puzzle about the lifts in a hotel which serve floors based on the day of the week.

Add together the dates of all the Thursdays in May this year. Which day sum is largest?

Which numbers when multiplied by the number of letters in the word(s) of the number give square numbers?

Arrange the numbers 1-9 to make three 3 digit numbers that add up to 999.

Investigate three fractions which add together to give one fifth.

Investigate three fractions which add together to give one ninth.

Find other numbers that can be changed to 1 on a calculator using only the 4 key and any operation.

A number puzzle suitable for children with a wide range of abilities.

Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.

Arrange the numbers on the grid of squares so that the totals along each line of three squares are equal.

Place the numbers on the triangle so that the totals along each of the sides are equal.

Find calculations which written back to front give the same answer.
Exercises
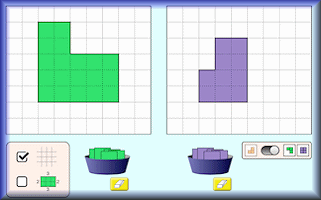
Area Builder
An interactive workspace in which to make shapes using square tiles with given areas and perimeters.
Area Two
How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?

Frustration
A logic challenge requiring a strategy to update each of the numbers in a grid.
Function Builder
An interactive function machine for patterns, numbers and equations.
Graph Plotter
An online tool to draw, display and investigate graphs of many different kinds.
Green Fingers
Choose the amount of liquid from each bottle needed to make the watermelon grow as big as possible.

Happy Numbers
To find out whether a number is happy square each of its digits, add the answers and repeat. End in one and the number is happy.

Jugs
Can you make four litres if you only have seven and five litre jugs?
Largest Product
A drag and drop activity challenging you to arrange the digits to produce the largest possible product.

Leapfrog
An investigation of the minimum number of moves required to make the blue and green frogs swap places.

Maths Mind Reader
Investigate this amazing mind reading performance based on simple mathematical principles.

Mystic Rose
Investigate the properties of the Mystic Rose by using this interactive diagram.

Prison Cell Problem
A number patterns investigation involving prisoners and prison guards.

River Crossing
The traditional River Crossing challenge. Can you do it in the smallest number of moves?

Six Keys
Use just six keys on your calculator to make a given total. How many different ways can it be done?

Take Baht
How many different ways can you make a given total with Thai coins?
Other activities for this topic | | |
Complete Index of Starters
Search
The activity you are looking for may have been classified in a different way from the way you were expecting. You can search the whole of Transum Maths by using the box below.
Have today's Starter of the Day as your default homepage. Copy the URL below then select
Tools > Internet Options (Internet Explorer) then paste the URL into the homepage field.
Set as your homepage (if you are using Internet Explorer)
Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world.
Click here to enter your comments.