Triangle Solver

Drag the vertices to make the triangle roughly the shape you want.

At least one vertex must be moved before entering the triangle's data.

Click on three labels and enter the size of the angle or side.

Label the vertices     ,         and        

When you have entered three attributes click the button below:

How to Solve a Triangle

In order to find all the attributes of a triangle at least three measurements are needed. In fact only three measurements are needed unless they are the three angles. In that case it is impossible to determine the lengths of the sides and the area as there are an infinite number of similar triangles with thise same three angles.

The following three relationships are used to find the unknown sides and angles.

Sine Rule

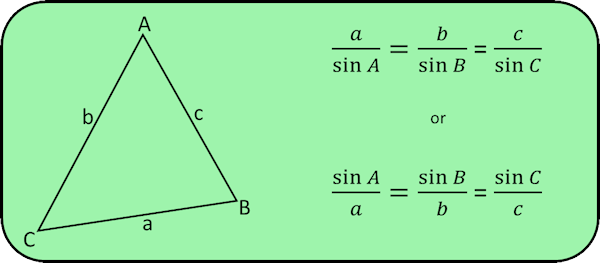
Cosine Rule

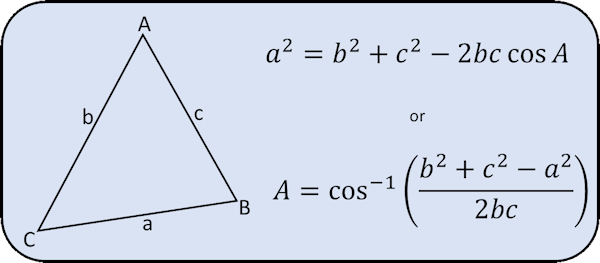
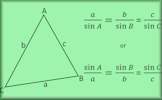
Sine Formula

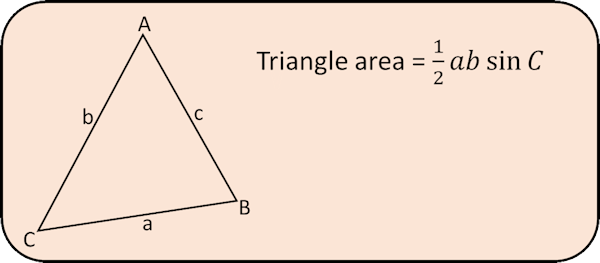
Input

The lengths of sides and size of angles must be all be positive numbers. Each angle must be less than 180^o and the longest side must be less than the sum of the shorter two sides.

Construction

This Solver is not only intended to be used with standard trigonometry or Pythagoras questions but also as a resource for students learning the basic construction skills with a rulers and pair of compasses. It also works well for a class practicing drawing angles using a protractor.

The teacher could manipulate the triangle above to show a base of say 13cm. Either side of this base angles of 50° and 70° are shown. The class is then challenged to make an accurate drawing of the triangle and their accuracy can be measured against the actual values the Triangle Solver produces when everyone has finished their drawings.

Similarly a triangle with only the three sides given can be projected for a class practicing ruler and compass constructions. This time it is fun to compare the measured angles of the finished triangle with the ones the Triangle Solver calculates.

Exercises

Suggested Trigonometry Right-angled triangle trigonometry questions starting with the basics then going on to 3D and exam-style questions. The short web address is: Transum.org/go/?to=trig

Suggested Common Trig Ratios A self-marking exercise covering the common trigonometric ratios for certain memorable angles. The short web address is: Transum.org/go/?to=commontrigratios

Suggested Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle. The short web address is: Transum.org/go/?to=adtrig

Cheating

Dear students, this tool is designed to enhance your understanding of trigonometry and to validate your calculations. While it can provide answers, solely relying on it for your homework bypasses the valuable learning process. We encourage you to first attempt your assignments independently, then use this app to verify your solutions. If discrepancies arise, consult with your teacher to bridge the gaps in your understanding. Remember, the journey of learning is as crucial as the destination.

Comments

Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.