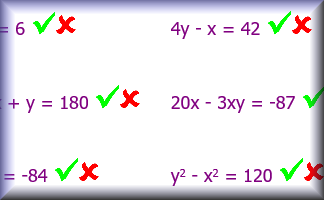There are of course no end of correct answers and here are some examples.
There is at least one mistake. Can you find the errors when x=3 and y=4?
| \(x + y = 8\) | \(x - y = -1\) | \(y - x = 1\) |
| \(2x + 3y = 18\) | \(5x - 2y = 7\) | \(4y - x = 13\) |
| \(xy - 10 = 2\) | \(180 - 2x + y = 186\) | \(20x - 3xy = 24\) |
| \(x^2 + y = 13\) | \(10x - y^2 = 14\) | \(y^2 - x^2 = 7\) |
| \(x^2y + 13 = 49\) | \(x^2y^2 - 2x = 138\) | \(x^2y^2 = 576\) |
| \(x! + y = 10\) | \(5(x + y) = 35\) | \(3y \div x = 22\) |
| \(\frac{xy}{2}= 25\) | \(\frac{84}{xy}= 7\) | \(\frac{36y}{5x}= y\) |
Note to teacher: Doing this activity once with a class helps students develop strategies. It is only when they do this activity a second time that they will have the opportunity to practise those strategies. That is when the learning is consolidated. Click the button above to regenerate another version of this starter from random numbers.
|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=April20 However it would be better to assign one of the student interactive activities below. |
|
Here is the URL which will take them to a related student activity.
Sign in to your Transum subscription account to see the answers
Curriculum Reference
See the National Curriculum page for links to related online activities and resources.
