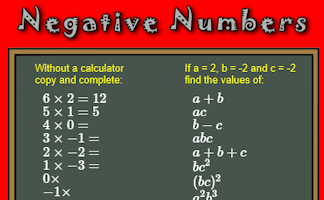Number Starters:

Four different actions depending on the number which appears.

A game based around the concept of factors and abundant numbers.
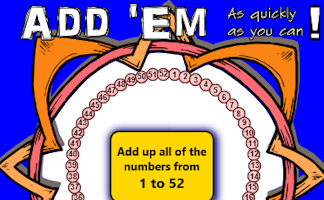
Add up a sequence of consecutive numbers. Can you find a quick way to do it?

Add up all the multiples of nine in an elegant way.

This activity requires students to memorise fifteen numbers in a three by five grid.

Work out the number of stamps needed to post a parcel.

Work out the date Will was born by answering some number questions.

Recognise odd, even, square, prime and triangular numbers.

If all the bells ring together at noon, at what time will they next all ring together? This problem requires the use of LCM.

Is there a pattern in the number of palindromic numbers to be found less than powers of 10?

Can you use the digits on the left of this clock along with any mathematical operations to equal the digits on the right?

Fifteen pennies are placed in four envelopes and the envelopes are sealed. It is possible to pay someone any amount from 1p to 15p by giving them one or more envelopes.

Work out how many people were at the dance from the clues given.

Determine whether the given nets would fold to produce a dice.

Arrange the digits from 1 to 9 in alphabetical order. How many times can this number be halved?

How old is a person if when her age is divided by certain numbers, the calculator display ending are as shown.

Begin with one, double it, double it again and so on. How many numbers in this sequence can you write down before the register has been called?

Spot the factors and the multiples amongst the numbers in the grid.

If each number in a sequence must be a factor or multiple of the previous number what is the longest sequence that can be made from the given numbers?
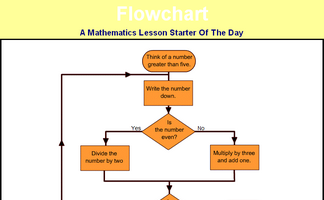
Use the flowchart to generate a sequence of numbers. Which number will reach 1 the fastest?
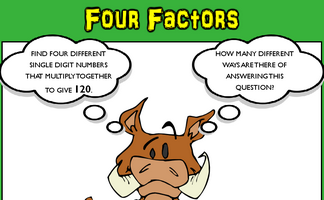
Find four single digit numbers that multiply together to give 120. How many different ways are there of answering this question?

For mathematical questions to get everyone thinking at the beginning of the lesson.

Start with 512. Halve it to get 256. Halve it to get 128. Continue as far as possible.

If all the students in this room shook hands with each other, how many handshakes would there be altogether?

Move the numbered cards to form five 2 digit numbers which are all multiples of three.

A puzzle about the lifts in a hotel which serve floors based on the day of the week.

The numbers on five houses next to each other add up to 70. What are those five numbers?

Write down as many multiples of 3.5 as possible in 3.5 minutes.

The 31st of December is the last day of the year. What mathematical lasts do you know?

A question about the birthdays of a child born on the 29th February.

Questions about the number of letters in numbers.

Which numbers when multiplied by the number of letters in the word(s) of the number give square numbers?

Find the missing terms from these linear sequences.

Work out what the nth letter will be in a recurring pattern of letters in a person's name
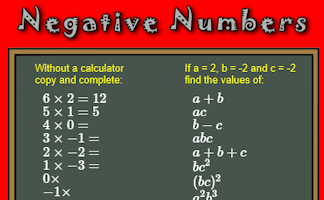
Perform calculations involving negative numbers

Find which numbers in a given list do not combine with other numbers on the list to make a given sum.

Can you work out the numbers from the given clues.

Write out in words some numbers writen as digits (optional pirate theme)

From the numbers given, find the one that is the odd one out.

Find other numbers that can be changed to 1 on a calculator using only the 4 key and any operation.

Find three numbers such that each pair of numbers adds up to a square number.

Six is a perfect number as it is the sum of its factors. Can you find any other perfect numbers?

Arrange numbers on the plane shaped grid to produce the given totals

Arrange numbers at the bottom of the pyramid which will give the largest total at the top.

When the register is called answer with a multiple of 7.

Arrange the numbers on the snowballs so that no two consecutive numbers are directly connected by rope.
Rearrange the numbers, row and column headings so that this table is mathematically correct.

Can you work out from the five clues given what the mystery number is?

How many square numbers can be found in the grid of digits.
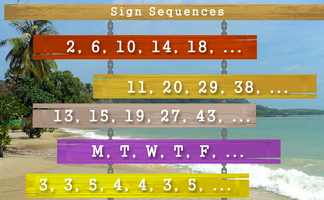
Continue the sequences if you can work out the rule.

The classic game of Nim played with a group of pens and pencils. The game can be extended to the multi-pile version.

Arrange the digits one to nine in the grid so that they obey the row and column headings.

Arrange the numbers on the cards so that each of the three digit numbers formed horizontally are square numbers and each of the three digit numbers formed vertically are even.
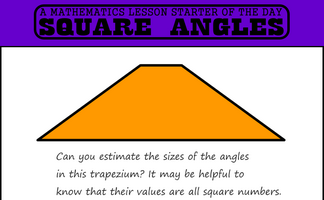
Find a trapezium, a triangle and a quadrilateral where all of the angles are square numbers.

Draw a picture of a Christmas tree using only square numbers.

Arrange the numbered trees so that adjacent sums are square numbers.

Write out as many square numbers as possible in 4 minutes.

A challenge to find numbers which have each of their digits as square numbers.

Find a power of 2 and a power of 3 that are consecutive numbers.

Be creative and come up with as many facts about a number as you can think of.

How can you put the dice into the tins so that there is an odd number of dice in each tin?

A Maths puzzle based on the 12 Days of Christmas song.

Find the two numbers whose sum and product are given.
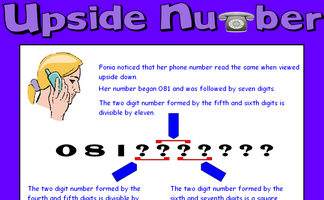
Work out the phone number from the clues given.
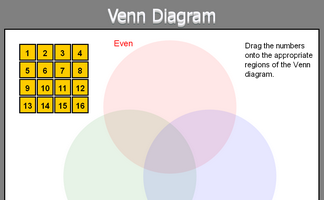
Arrange numbers on the Venn Diagram according to their properties.

A starter about sums, products, differences, ratios, square and prime numbers.
Advanced Number Starters
Exercises
Binary Lights
Represent binary numbers with a row of ligts which can be turned on or off.

Binary Numbers
Learn how to convert numbers from decimal to binary and from binary to decimal.

Chinese Numbers Jigsaw
An online interactive jigsaw puzzle of a grid of Chinese number symbols.

Consecutive Numbers
Find the consective numbers that are added or multiplied to give the given totals
Counter
A dynamic visual aid that counts! Choose the first term, common difference and the speed

Counting Quest
Try this exercise to master counting up to 100 items with precision and confidence.

Delightfully Divisible
Arrange the digits one to nine to make a number which is divisible in the way described.
Dice Net Challenge
Drag the numbers onto the net so that when it is folded to form a cube numbers on opposite faces add up to prime numbers.

Digimoji
Crack the emoji code by testing equations and spotting patterns.

Divisibility Test
Practise using the quick ways to spot whether a number is divisible by the digits two to nine.
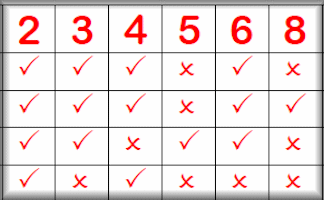
Divisibility Tests 2-12
A visual aid designed to be projected in the classroom. Here you can find the quick ways of telling whether a number is exactly divisible by the numbers two to twelve.

Don't Shoot The Square
You will need to be quick on the draw to shoot all of the numbers except the square numbers.

Dump-A-Dice Race
An online board game for two players involving prime and square numbers and making choices.
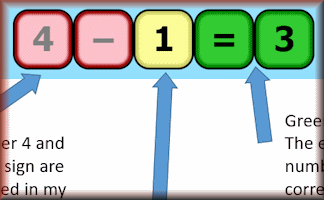
Equatero
Find the expression from a series of guesses and clues.
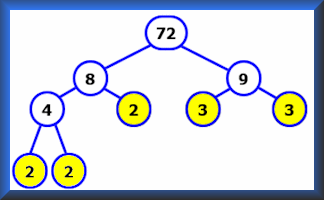
Factor Trees
Create factor trees to find the prime factors of the given numbers.

Fizz Buzzer
The digital version of the popular fizz buzz game. Press the buzzers if they are factors of the counter.

Formal Written Methods
Examples of formal written methods for addition, subtraction, multiplication and division.

Goal Products
Arrange the numbered footballs on the goal posts to make three, 3-number products that are all the same.

HCF and LCM
Practise finding the highest common factor (H.C.F), sometimes called the greatest common divisor, and the lowest common multiple (L.C.M) of two numbers.
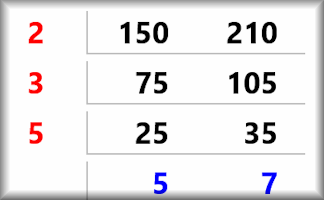
HCF and LCM Calculator
A demonstration of how to find the highest common factor (HCF or GCD) and the lowest common multiple (LCM) of two numbers.

Hot Number Challenges
These hot numbers challenges are for students with no access to a computer and are presented in a form suitable to be projected onto a whiteboard in front of a class.

Hot Numbers
Move the numbered cards to form five 2-digit numbers which obey the given rules. A ten-stage numeracy challenge.

Knowing Numbers
Read, write, order and compare numbers from one to twenty.

Leapfrog
An investigation of the minimum number of moves required to make the blue and green frogs swap places.
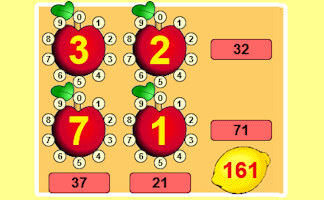
Lemon Law
Change the numbers on the apples so that the number on the lemon is the given total.
Magic Square Puzzle
Find all of the possible ways of making the magic total from the numbers in this four by four magic square.

Maths Mind Reader
Investigate this amazing mind reading performance based on simple mathematical principles.

Missing Terms
Can you work out which numbers are missing from these number sequences?

Mix and Math
Determine the nature of adding, subtracting and multiplying numbers with specific properties.
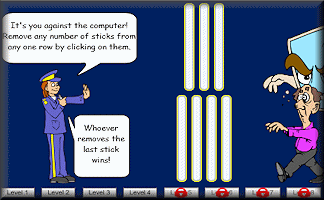
Nim
Nim is a mathematical game of strategy in which two players take turns removing objects from groups of objects.

No Partner
Find which numbers in a given list do not combine with other numbers on the list to make a given sum.
Number Grids
Investigate the properties of number with these interactive number grids.
Number Jigsaws
Online, interactive jigsaw puzzles of grids of numbers.
Number Line
This number line visual aid is designed to be projected onto a whiteboard for whole class exposition.

Number Rhyme
A poem about the numbers one to nine. Just for fun can you make up a last line for each verse?

Number Skills Inventory
A checklist of basic numeracy techniques that every pupil should know.
Number Systems
Place the numbers in the correct sets in this concentric circles Venn diagram.

Numbersina
Show that you know how many whatsits are in a thingamabob and other 'Numbers In A ...' answers.

Pairs 240
Find the pairs of numbers that multiply together to give a product of 240 in this collection of matching games.

Pandigital Numbers
An exercise exploring the properties of nine-digit numbers containing each of the digits 1 to 9.

Pascal's Patterns
See the number patterns on Pascal's Triangle with this colourful, interactive application.

Pascal's Triangle
Get to know this famous number pattern with some revealing learning activities

Pesto
Students classify numbers randomly appearing on the screen by holding up cards

Pick The Primes
Pick the prime fruit from the tree as quickly as possible. Practise to improve your personal best time.

Plane Numbers
Arrange numbers on the plane shaped grid to produce the given totals

Playing Card Maths
Imagine you are on a desert island with nothing but a pack of playing cards. Do you have to stop learning mathematics?

Powten
Practise multiplying and dividing by powers of ten without using a calculator.
Prime Labyrinth
Find the path to the centre of the labyrinth by moving along the prime numbers.
Prime Numbers Jigsaw
Interactive jigsaw puzzles of different types of grids containing prime numbers.

Prime Pairs Game
A game for two players who take turns to select two numbers that add up to a prime number.
Prime Path Pace
The objective is to find a continuous path of prime numbers in the shortest time.

Prime Prevention
Players take turns placing numbers from 1-9 on the grid. Avoid making three-digit prime numbers in any direction!

Prime Square
Drag the numbers into the red cells so that the sum of the three numbers in each row and each column is a prime number.

Prison Cell Problem
A number patterns investigation involving prisoners and prison guards.
Product of Primes
Match the primes that multiply to give the products. A drag and drop activity.
Product Square
Arrange the given numbers in a three by three grid to obtain the diagonal, row and column products.

River Crossing
The traditional River Crossing challenge. Can you do it in the smallest number of moves?
Roman Numerals Jigsaw
An online interactive jigsaw puzzle of a grid of Roman numerals.
Roman Numerals Quiz
This online, self marking quiz tests your ability to convert Roman numerals.
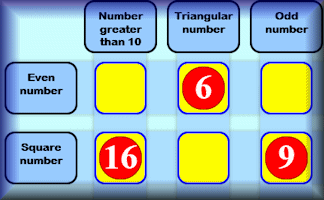
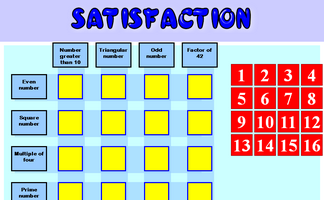
Satisfaction
This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers.
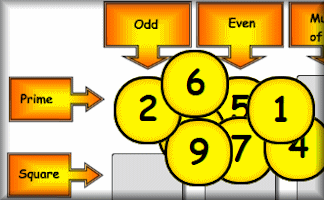
Satisfy
Place the nine numbers in the table so they obey the row and column headings about the properties of the numbers.
Scallywags and Scoundrels
Arrange the scallywags and scoundrels on the chairs so that the numbers of any two sitting next to each other add up to a prime number.
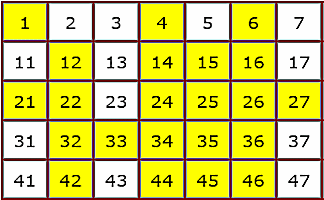
Sieve of Eratosthenes
A self checking, interactive version of the Sieve of Eratosthenes method of finding prime numbers.
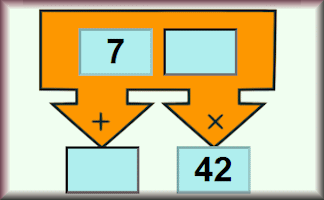
Some Sums and Products
Number puzzles involving adding, multiplying and problem solving

Square and Even
Arrange the numbers on the cards so that each of the three digit numbers formed horizontally are square numbers and each of the three digit numbers formed vertically are even.

Square Numbers
Calculate the squares of one-digit and two-digit numbers.
Square Pairs Game
A game for two players who take turns to select two numbers that add up to a square number.

Suko Sujiko
Interactive number-based logic puzzles similar to those featuring in daily newspapers.

Thai Numbers Jigsaw
An online interactive jigsaw puzzle of a grid of Thai number symbols.

Three Prime Sum
A self-marking challenge to write each of the given numbers as the sum of three prime numbers.

Three Ways
Find three different ways of multiplying four different digits together to get the given target number. There are nine levels for this online challenge.
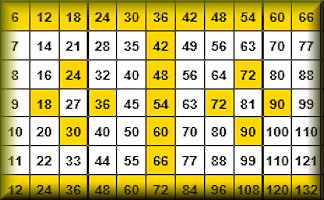
Times Square
Practise your times tables with this self-checking multiplication grid.

Times Tables
A collection of activities to help you learn your times tables in only 5 days.
Twelve Days
How many gifts did my true love send to me according to the traditional Christmas song 'Twelve Days of Christmas'.
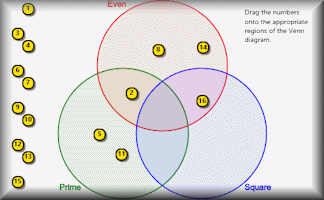
Venn Diagram
Place each of the numbers 1 to 16 on the correct regions on the Venn diagram.
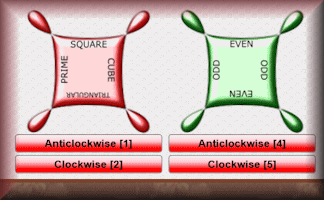
Watsadoo
Rotate the cogs to catch the flying numbers in the correct sections.

What Are They?
An online exercise about sums, products, differences, ratios, square and prime numbers.
Other activities for this topic | | |
Complete Index of Starters