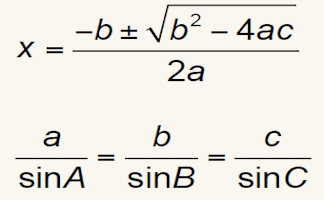Mensuration Starters:

How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
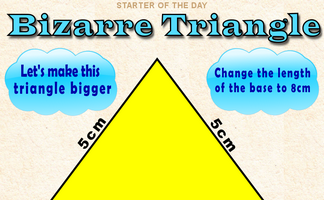
By how much would the area of this triangle increase if its base was enlarged to 8cm?

Which of the two shapes has the largest area? You will be surprised!
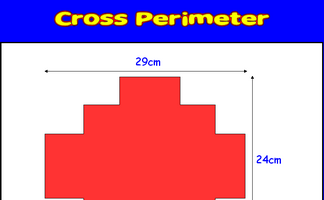
Calculate the distance around the given shape
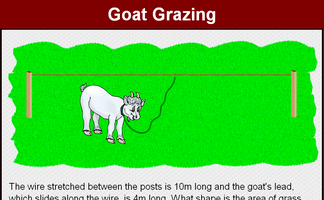
Find the loci of the goat's position as it eats the grass while tethered to the rope.

Introduce linear equations by solving these problems about lengths.

The missing square puzzle is an optical illusion used to help students reason about geometrical figures.

Find the dimensions of a rectangle given the perimeter and area.

Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.

A quick quiz about five items on a shopping list written 40 years ago.
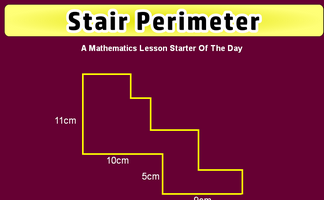
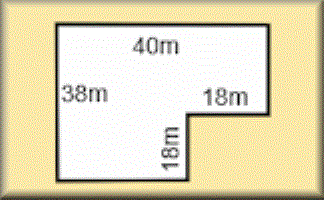
Use the information implied in the diagram to calculate the perimeter of this shape.

Is it possible to work out the perimeter of this shape if not all the side lengths are given?
Exercises
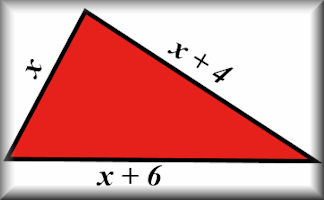
Algebraic Perimeters
Questions about the perimeters and areas of polygons given as algebraic expressions.

Animal Records
Match the values and the units to the animal world records.
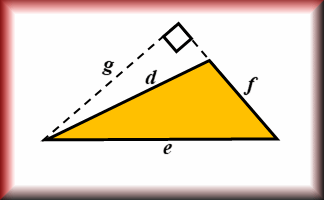
Area and Perimeter
Show that you know the area and perimeter formulas of basic shapes.
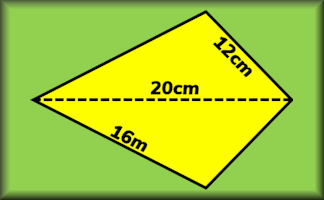
Area and Perimeter of a Kite
A short exercise to practise using the formulae for area and perimeter of a kite.

Area and Perimeter of a Parallelogram
Many different ways to practise your skills finding the areas and perimeters of parallelograms.
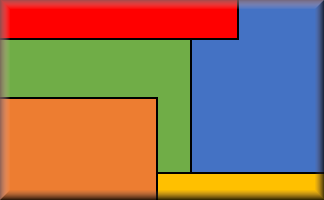
Area and Perimeter of a Rectangle
Questions on the areas and perimeters of rectangles which will test your problem solving abilities.
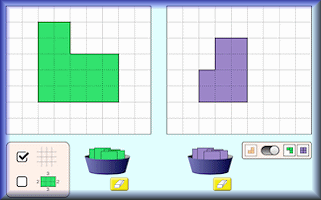
Area Builder
An interactive workspace in which to make shapes using square tiles with given areas and perimeters.
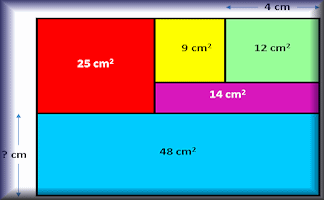
Area Maze
Use your knowledge of rectangle areas to calculate the missing measurement of these composite diagrams.
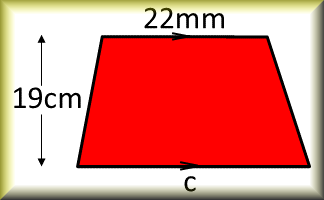
Area of a Trapezium
Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.
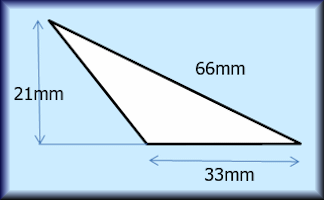
Area of a Triangle
Calculate the areas of the given triangles in this self marking quiz.
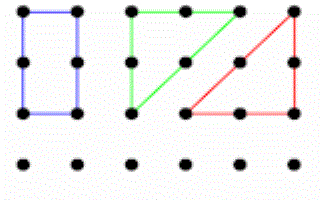
Area Two
How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
Areas of Composite Shapes
Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.

Bottles, Boxes and Cans
Estimate the capacity of the bottles, boxes and cans in the photograph and answer questions about volume.

Circles
Practise using pi to calculate various circle measurements. There are six levels of difficulty.

Compound Units
Practise using compound units such as speed, unit pricing and density to solve problems.

Converting Metric Units
Converting metric measurements of length, mass, volume and time from one unit of measure to another.

Cylinders
Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions
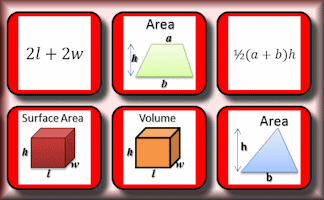
Formulae Pairs
Find the matching pairs of diagrams and formulae for basic geometrical shapes.
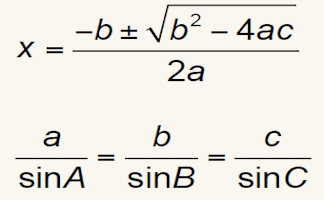
Formulae to Remember
The traditional pairs or pelmanism game adapted to test recognition for formulae required to be memorised for GCSE exams.
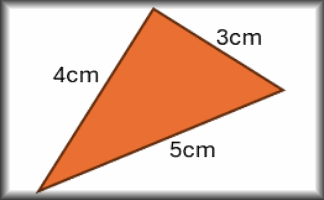
Heron's Formula
Use the lengths of the three sides of a triangle to calculate the area.

Imperial Units
Learn about common imperial units and how they relate to other units of measurement.

Imperial Units Pairs
Find the matching pairs of equivalent imperial units in this interactive online game.

Inequalities
Check that you know what inequality signs mean and how they are used to compare two quantities. Includes negative numbers, decimals, fractions and metric measures.
Map Scales
Test your understanding of map scales expressed as ratios with this self marking quiz.
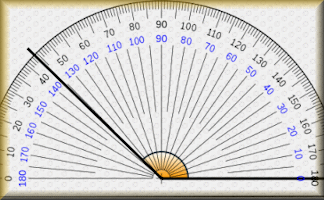
Measuring Angles
Measure the size of the given angles to within two degrees of their actual value.

Measuring Units
Check your knowledge of the units used for measuring with this self-marking quiz about metric and imperial units.

Memorable Measures
This is a visual aid and printable cards to introduce a homework activity about measures.

Metric Units Pairs
Find the matching pairs of equivalent metric units in this interactive online game.

Mileometer
Practise converting between miles and kilometres with this self marking quiz.
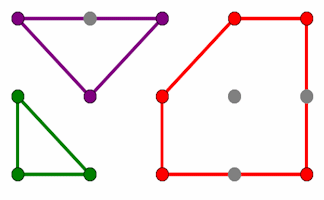
Pin Board
Rows and columns of dots that can be joined using straight lines to create shapes.
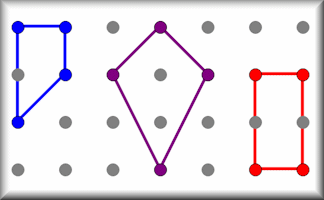
Quad Areas
Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
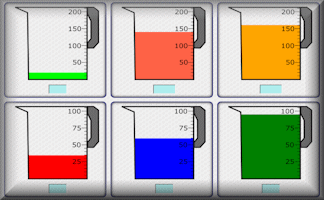
Reading Scales
A self marking exercise on the reading of scales of different types.

Scale Drawings
Measure line segments and angles in geometric figures, including interpreting scale drawings.

Scale Setting
Move the pointer along the scale to show the given reading.

Screen Test
Memorise the mathematical facts in the video then answer the ten quiz questions.
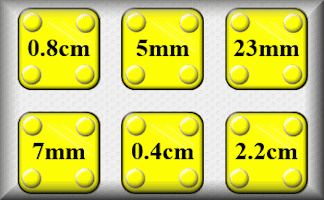
Sorting Units
Order the ten containers according to their value (money, length and weight)
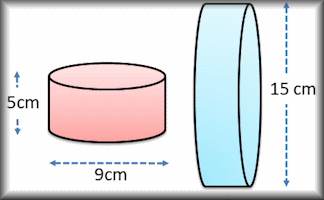
Surface Area
Work out the surface areas of common solid shapes in this collection of exercises.
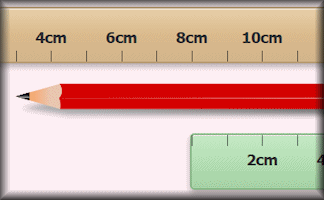
Two Measures
Calculate the length of the item based on other given measurements.
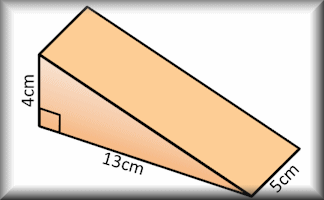
Volume
Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.

Volume Equals Surface Area
Find the cuboids with integer side lengths where the volume is numerically equal to the surface area.
Other activities for this topic | | |
Complete Index of Starters