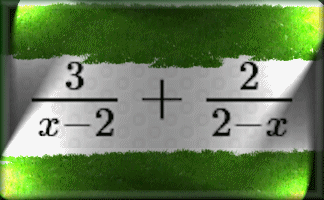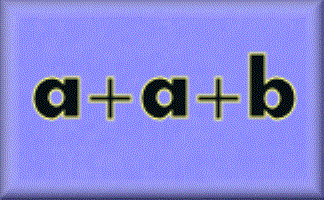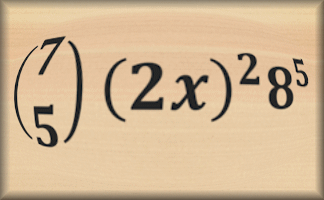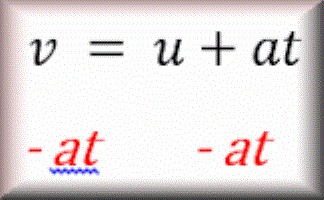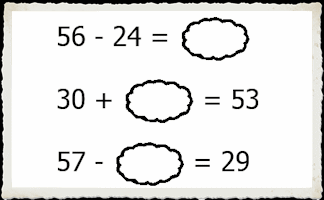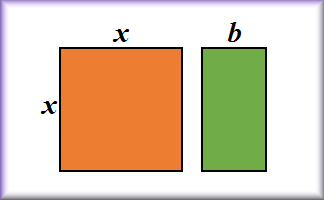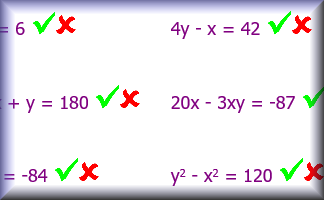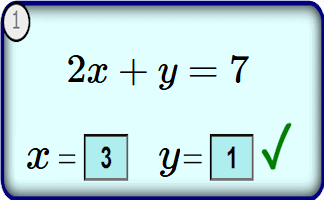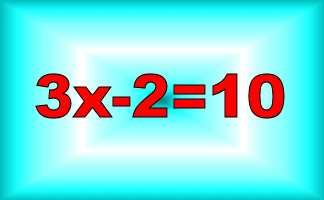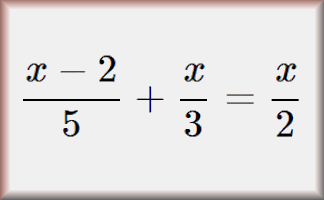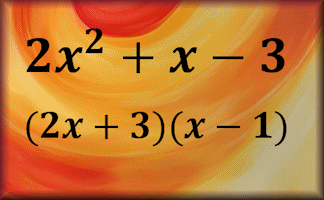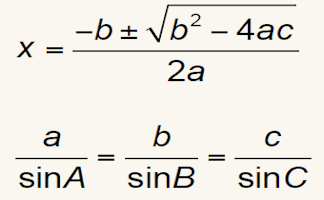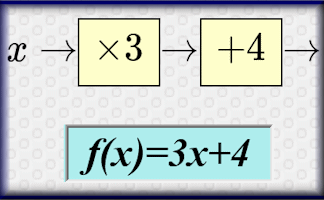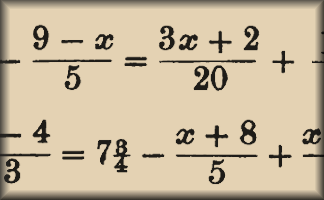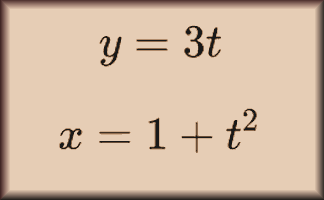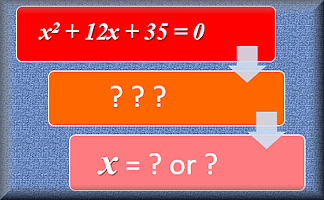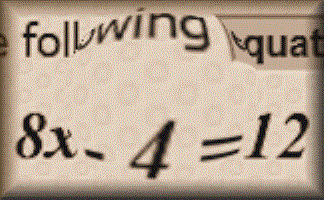Algebra Starters:
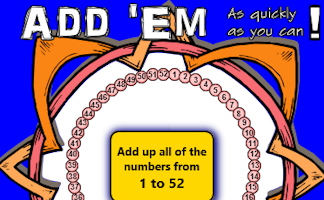
Add up a sequence of consecutive numbers. Can you find a quick way to do it?

This lesson starter requires pupils to find the missing numbers in this partly completed arithmagon puzzle.

You have four minutes to write down as many equations as you can involving B, T and S.

Calculate the total cost of four cars from the information given.

Work out the number of chin ups the characters do on the last day of the week give information about averages.

Work out the total cost of five Christmas presents from the information given.
Give 20 rules connecting x and y given their values.

The height of this giraffe is three and a half metres plus half of its height. How tall is the giraffe?

Find the number which when added to the top (numerator) and bottom (denominator) of each fraction make it equivalent to one half.

Check a student's homework. If you find any of the answers are wrong write down a sentence or two explaining what he did wrong.

Find the weight of one cuboid (by division) of each colour then add your answers together.

Change the numbers on the apples so that the number on the lemon is the given total.

This mathematics lesson starter invites pupils to interpret a three part algebraic inequality.

A lamp and a bulb together cost 32 pounds. The lamp costs 30 pounds more than the bulb. How much does the bulb cost?

Which algebraic expression is the odd one out?

Introduce linear equations by solving these problems about lengths.

Work out why subtracting a two digit number from its reverse gives a multiple of nine.

Practise techniques for answering questions involving negative numbers.

The sum and product are given, can you find the two numbers?

You have four minutes to write down as many equations as you can involving the given letters.

Arrange numbers at the bottom of the pyramid which will give the largest total at the top.

There are some rabbits and chickens in a field. Calculate how many of each given the number of heads and feet.

Use the weights of the trains to work out the weight of a locomotive and a coach. A real situation which produces simultaneous equations.

It is called Refreshing Revision because every time you refresh the page you get different revision questions.

A problem involving two people's ages which can be solved using algebra.

Work out the number of clowns and horses given the number of heads and feet.

A question which can be best answered by using algebra.

A problem which can best be solved as a pair of simultaneous equations.
Solve these balance puzzles by taking the same away from both sides. An introduction to linear equations.
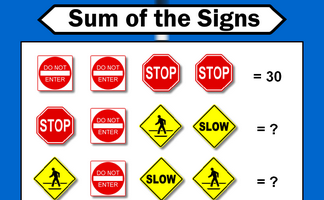
Each traffic sign stands for a number. Some of the sums of rows and columns are shown. What numbers might the signs stand for?

How many children and how many donkeys are on the beach? You can work it out from the number of heads and the number of feet!

A problem which can be answered by forming an algebraic equation then solving it.

THOAN stands for 'Think of a number' and there are four randomly generated THOAN puzzles to solve.

A Think Of A Number problem presented as a news ticker.
Advanced Algebra Starters
Exercises
Algebra In Action
Real life problems adapted from an old Mathematics textbook which can be solved using algebra.

Algebra Pairs
The classic Pelmanism or pairs game requiring you to match equivalent expressions.
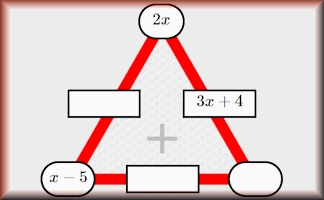
Algebragons
Find the missing expressions in these partly completed algebraic arithmagon puzzles.
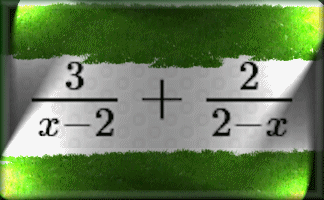
Algebraic Fractions
A mixture of algebraic fraction calculations and simplifications.

Algebraic HCF
Exercises providing practice finding the highest common factor of algebraic expressions.

Algebraic LCM
Exercises providing practice finding the lowest common multiple of algebraic expressions.
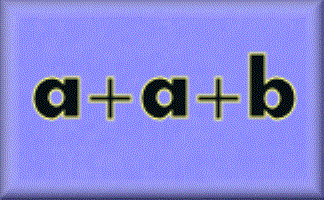
Algebraic Notation
Simplification using the normal conventions of algebra.
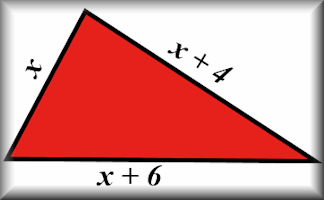
Algebraic Perimeters
Questions about the perimeters and areas of polygons given as algebraic expressions.

BIDMAS
A self marking exercise testing the application of BIDMAS, an acronym describing the order of operations used when evaluating expressions.

BIDMAS Game
An online interactive game celebrating the order of mathematical operations.
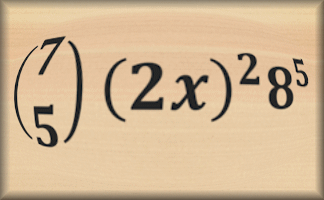
Binomial Theorem
Exercises in the process of expanding powers of binomial expressions and finding specific coefficients.

Brackets
Expand algebraic expressions containing brackets and simplify the resulting expression in this self marking exercise.
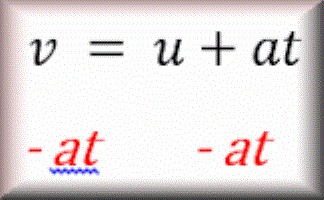
Changing The Subject
Rearrange a formula in order to find a new subject in this self marking exercise.
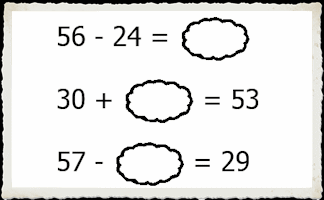
Clouds
Can you work out which numbers are hidden behind the clouds in these calculations?
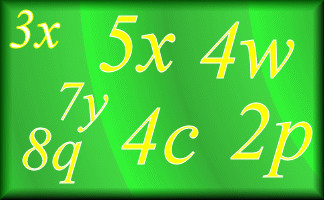
Collecting Like Terms
Practise your algebraic simplification skills with this self marking exercise.
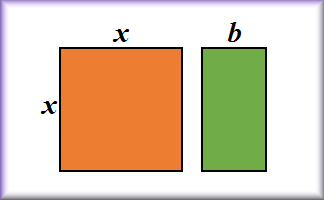
Completing the Square
Practise this technique for solving quadratic equations and analysing graphs.
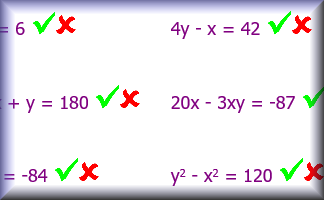
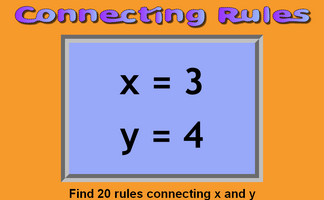
Connecting Rules
If you are given the values of x and y which of these equations is correct?
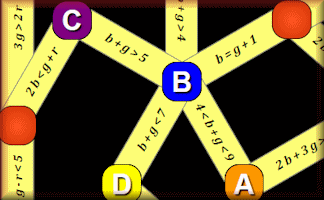
DiceGebra
An online board game for two players evaluating algebraic equations and inequalities.
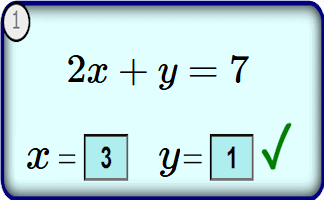
Diophantine Equations
Practise finding integer solutions to equations with more than one unknown.

eQuation Generator
An unlimited supply of linear equations just waiting to be solved. Project for the whole class to see then insert the working in your own style.
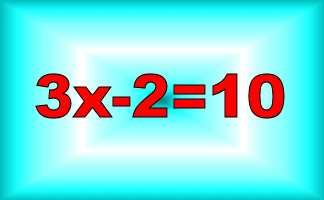
Equations
A series of exercises, in increasing order of difficulty, requiring you to solve linear equations. The exercises are self marking.
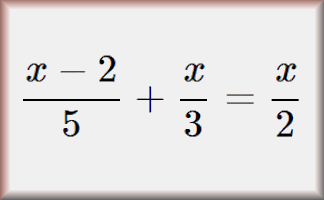
Equations with Fractions
Practise solving linear equations that contain fractions in this multi-level exercise.
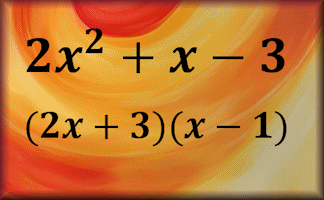
Factorising
Practise the skills of algebraic factorisation in this structured online self-marking exercise.
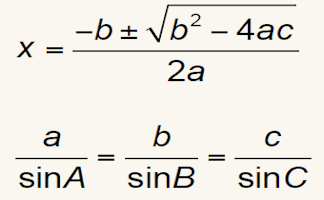
Formulae to Remember
The traditional pairs or pelmanism game adapted to test recognition for formulae required to be memorised for GCSE exams.
Function Builder
An interactive function machine for patterns, numbers and equations.
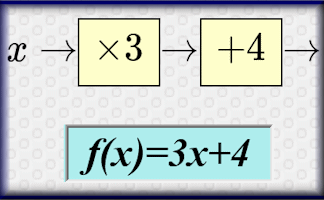
Functions
An online exercise on function notation, inverse functions and composite functions.
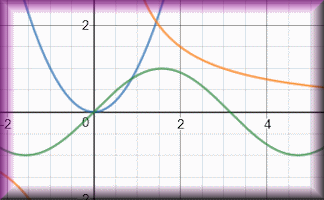
Graph Equation Pairs
Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function.

How old was Diophantus?
An ancient riddle which can be answered by solving an equation containing fractions.
Identity, Equation or Formula?
Arrange the given statements in groups to show whether they are identities, equations or formulae.

Inequalities
Check that you know what inequality signs mean and how they are used to compare two quantities. Includes negative numbers, decimals, fractions and metric measures.

Iteration
Find approximate solutions to equations numerically using iteration.
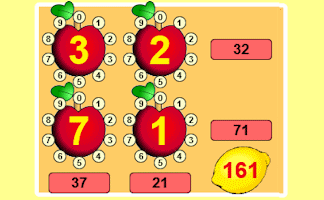
Lemon Law
Change the numbers on the apples so that the number on the lemon is the given total.
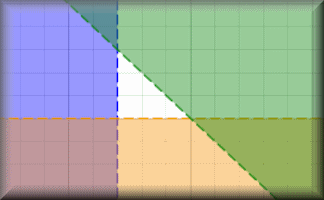
Linear Programming
A selection of linear programming questions with an interactive graph plotting tool.
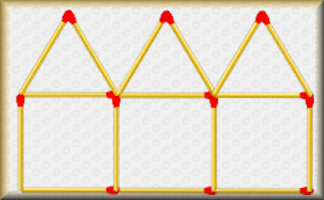
Matchstick Patterns
Create a formula to describe the nth term of a sequence by examining the structure of the diagrams.
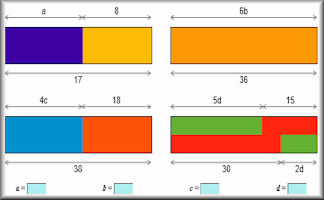
Missing Lengths
Find the unknown lengths in the given diagrams and learn some algebra at the same time.

Nevertheless
Players decide where to place the cards to make an equation with the largest possible solution.
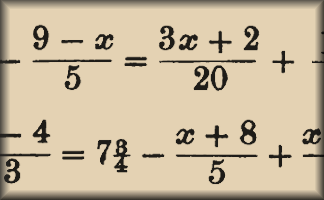
Old Equations
Solve these linear equations that appeared in a book called A Graduated Series of Exercises in Elementary Algebra by Rev George Farncomb Wright published in 1857.
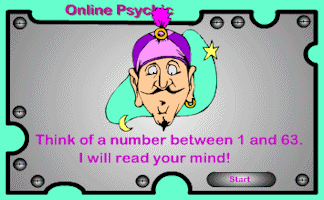
Online Psychic
Let the psychic read the cards and magically reveal the number you have secretly chosen. What is the mathematics that makes this trick work?
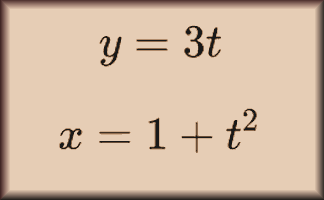
Parametric Equations
Develop the skills required to manipulate a set of equations involving a paramater.

Partial Fractions
Exercises on mastering the art of partial fraction decomposition.

Pascal's Triangle
Get to know this famous number pattern with some revealing learning activities

Polynomial Division
Practise dividing one algebraic expression by another in this set of exercises.
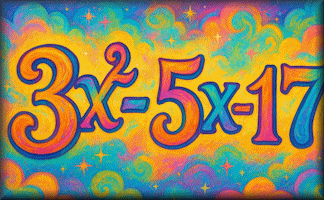
Problems Leading To Quadratics
Situations from 1885 which can be described using algebra and explained by solving quadratic equations
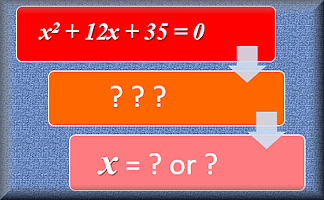
Quadratic Equations
Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.

Recurring Decimals
Change recurring decimals into their corresponding fractions and vica versa.

Simultaneous Equations
A self-marking, multi-level set of exercises on solving pairs of simultaneous equations.
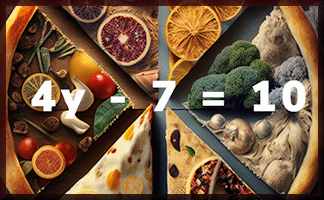
Solve To Find Fractions
Find the value of the unknown in each of these linear equations. All of the answers are fractions
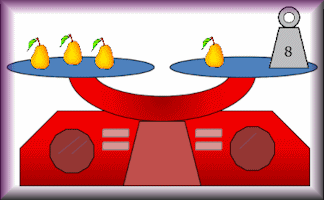
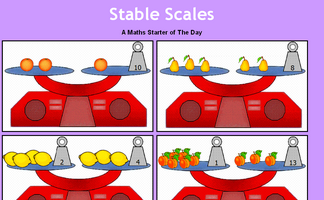
Stable Scales
Ten balance puzzles to prepare you for solving equations.

Substitution
Substitute the given values into the algebraic expressions.
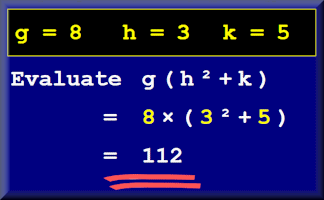
Substitution Examples
A projectable set of animated examples to help prepare pupils to do the Substitution online exercise.

Substitution Sort
Order the algebraic expressions according to their value with the given substitution.
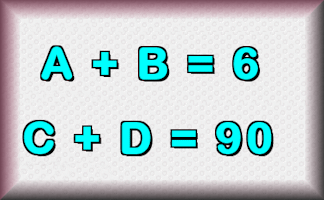
Superfluous
Find a strategy to figure out the values of the letters used in these calculations.

Think of a Number
Ten students think of a number then perform various operations on that number. You have to find what the original numbers were.
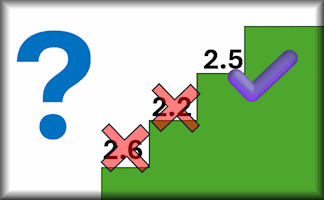
Trial And Improvement
Learn efficient ways of using trial and improvement to solve real-life and algebraic problems.
Where am I with Algebra?
Find out how developed your algebra skills are and then take them to the next level.
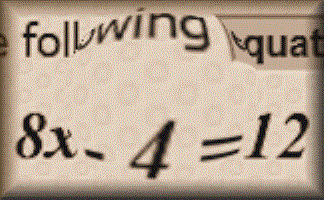
Words and Concepts
Fill in the missing words to show an understanding of the vocabulary of equations, inequalities, angles and shapes.

Writing Expressions
Listen to the voice saying the algebraic expression then write it in its simplest form.
Other activities for this topic | | |
Complete Index of Starters