Drawing 3D Objects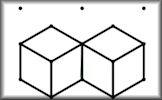
Draw two-dimensional representations of three-dimensional objects on an isometric dotty grid.
Volume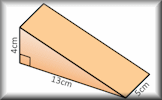
Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Net or Not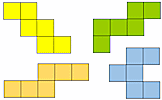
Drag the nets into the corresponding panels to show whether they would fold to form a cube.
Dice Net Challenge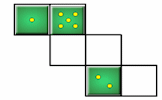
Drag the numbers onto the net so that when it is folded to form a cube numbers on opposite faces add up to prime numbers.
Cube Face Meetings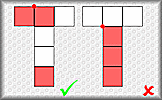
Visualise the cubes formed by the nets and paint the three faces meeting at a vertex.
Cubical Net Challenge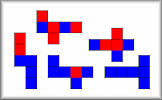
Find all the ways of painting the faces of cubes using only two colours.
Coloured Cube 3D
Colour in the remaining faces of the nets of the cubes to match the rotating three-dimensional picture.
Plans and Elevations
Interpret plans and elevations of three dimensional shapes.
Volume Equals Surface Area
Find the cuboids with integer side lengths where the volume is numerically equal to the surface area.
The Great Dodecahedron
Pupils are not allowed to use their hands to point but must describe fully any shapes they can see in this picture.
Puzzle Cube Net
A jumbled moving-block puzzle cube is shown as a net. Can you solve it?
Trigonometry in 3D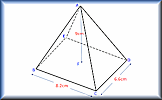
Calculate the lengths of sides and the size of angles in three dimensional shapes.
Faces, Edges and Vertices
Calculate the number of faces, edges and vertices on 3D Shapes.
Platonic Solids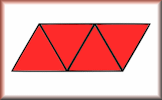
Identify the names, nets and features of the five regular polyhedra.
Similar Shapes
Questions about the scale factors of lengths, areas and volumes of similar shapes.
Cylinders
Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions
Surface Area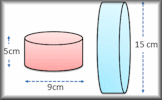
Work out the surface areas of common solid shapes in this collection of exercises.
Yes No Questions
A game to determine the mathematical item by asking questions that can only be answered yes or no.
Maxvoltray
Find the maximum volume of a tray made from an A4 sheet of paper. A practical mathematical investigation.
This is the main Transum help video on Shape (3D).
Volume Video
There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Platonic Solids Video
What are platonic solids and why are there only five of them?
Surface Area Video
Finding the surface are of three dimensional shapes can involve some interesting formulae.
Three Dimensional Trigonometry Video
When you have mastered trigonometry in two dimensions it is time to practise solving three-dimensional problems.
Tetrahedron and Pyramid
A tetrahedron and a pyramid have edges of equal length. If they are glued together on a triangular face with the vertices aligned, how many faces will the new shape have?
Cube Construction
This is a simple interactive that does nothing more than allow you to create 3D drawings of models made with cubes.
The Great Dodecahedron
Pupils are not allowed to use their hands to point but must describe fully any shapes they can see in this picture.
3D Trigonometry Presentation
A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes.
Dice Nets
Determine whether the given nets would fold to produce a dice.
Dice Reflections
A dice is reflected in two mirrors. What numbers can be seen?
Faces and Edges
Find the number of faces, edges and vertices on some familiar objects.
Icosahedron
How many triangles are there on the surface of a regular icosahedron.
28 items are currently in this category.
Teachers might find the complete Shape (3D) Topic List useful.
A particular skill is required to be able to excel in this area of Mathematics. Spatial awareness is important for solving multi-step problems that arise in areas such as architecture, engineering, science, art, games, and everyday life. Children have varying abilities visualizing three dimensional relationships but these abilities can be developed through practical activities and working through mathematical problems. Breaking down three dimensional situations into smaller two dimensional parts in an important strategy for problem solving.
See also the "Shape" Starters.
