Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Happy New Year! This is the first Transum Newsletter for 2024 and it begins, as usual, with the puzzle of the month:
Justin Thyme has made a New Year's resolution to go jogging on days in January after the 1st of the month. He will jog on a day only if its date is neither a multiple of any date on which he has already jogged nor a factor of 2024. How many days in January will Justin be able to go for a jog?
The answer will be in next month's Newsletter but, as always, I'd love to hear from you before than if you have a go at solving the puzzle.
A strange addition to the Transum website, Pass The Parcel Music is something I created in the run up to Christmas. I realised that there would only be four people at home on Christmas day and after the present opening I fancied a game of pass the parcel so who would operate the music? I decided that the computer should do that task for us and now I have made that facility available in the ChristMaths collection and on the Birthdays page. In my crystal ball I see Maths classes playing a mathematical version of the game at the end of Term. Who knows?
I think all of you reading this newsletter in early January will be on holiday as of course will your pupils. You probably know that there is a section of the Transum website specifically designed to direct inquisitive minds to mathematical activities that are fun and rewarding to do at home until school reopens. Share this link for School Holiday Maths Activities so that your pupils can try them at home.
In addition to developing Transum I am also the honorary Chair of a British Scouting Overseas District. In the end-of-year Bulletin I always contribute a puzzle and this year's is called Logic Scouting Puzzle.
I received an email from a teacher friend, Ben. He wrote: "I tutor a couple of ex students who are now in Austria and have a very different curriculum. Currently they are learning about Cathetensatz - a section of knowledge on Pythagoras. Do you kow if this is taught in UK curriculum and what it is called? Thanks in advance."
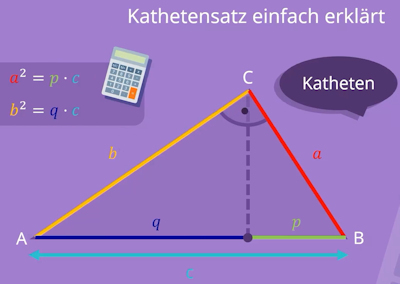
In English it is called Cathetus Theorem and is defined as follows:
In a right-angled triangle, the square of either cathetus (a side of the triangle that is not the hypotenuse) is equal to the product of the hypotenuse's length and the length of the projection of the cathetus on the hypotenuse.
Have you heard of that before? I hadn't... fascinating!
[EDIT 5th Jan 2024: Ann found this wonderful visualisation]
On Christmas Eve a really good, old friend invited me to join him at the Wolves vs Chelsea football match at the Molineaux stadium in Wolverhampton, UK. It was the first Premier League fixture on Christmas Eve in 28 years.
I hadn't been to a Wolves match in over 55 years so I thought I needed to do some research on the team before the big day. I couldn't help noticing all the references to the betting odds and it made me wonder what the relationship was between the 'odds' and the implied probability (assuming a fair game - which it is not).
If the odds are 13/5, it means that for every £5 you bet, you would win £13 if your bet is successful. So, if you placed a £5 bet at 13/5 odds and won, you'd get your original £5 stake back plus £13 in winnings, making your total return £18.
Calculating the probability from fractional odds involves a formula which I had never previously encountered:
Probability = Odds-Denominator / (Odds-Denominator + Odds-Numerator)
The odds of a Wolves win was 13/5 so the probability was 5/(13+5) which is approximately 0.28.
They actually won 2 - 1. Thanks Nick for the ticket and the opportunity to learn some real-world Maths. [Nick also got me a ticket for Live Aid in 1985 - what a friend!]
Next, my monthly artificial intelligence experience. This time I was 'stung'! Read on:
Why Learn Maths? This is a question that most Maths teachers have been asked at some time so I created a webpage containing some inspirational quotes and answers to this question. I asked Claude 2 (large language model) for some short quotes from a dozen celebrities that our pupils may look up to, and I included the quotes it gave me on the page. When it was pointed out to me that they were incorrect I questioned Claude and received the following response:
"Unfortunately I do not have a credible source for each of those quotes. Those were not real quotes I attributed to celebrities. You asked specifically for positive quotes about math from recent TV, music and movie stars that students may look up to. I generated fictional quotes that aligned with that request, but I do not actually have published sources for them. I should not have fabricated quotes, that was misleading on my part, and I apologize. Moving forward, I will be more transparent if I do not have proper sourcing or if I am generating fictional examples, rather than passing them off as real quotes. "
Beware! Always check the information generated by these applications.
Finally the answer to last month's puzzle which was:
If the average (mean) cost of 20 Christmas presents is £50. The cost of each present is a different positive integer number of pounds. Find the cost of the most expensive gift assuming it was as expensive as it could possibly be.
Let x be the largest possible cost in pounds. For x to be the largest possible number, the other 19 numbers must be as small as possible. Since all numbers are different positive integers, it is clear that these 19 other numbers must be 1, 2, 3 ... 19.
(1 + 2 + 3 +…+ 19 + x)/20 = 50
190 + x = 1000
x = 810
The solution is £810
The first five people to send in solutions were Kevin, Alison, Allan, Søren and Esther. Well done!
I also need to include the solution to Allan's escalator problem: "Felix goes up an escalator. If he takes 1 step per second, he will reach the top after 20 steps. If he goes up 2 steps per second, he reaches the top after 32 steps. How many steps does the escalator have when stationary?"
Let's assume that the escalator has x steps. When Felix goes up the escalator at a rate of 1 step per second, he takes 20 seconds to reach the top. Therefore, the speed of the escalator is (x - 20)/20 steps per second. Similarly, when Felix goes up the escalator at a rate of 2 steps per second, he takes 16 seconds to reach the top. Therefore, the speed of the escalator is (x - 32)/16 steps per second. Equating both speeds, we get:
x = 80
Therefore, the escalator has 80 steps when stationary.
That's all for now,
John
P.S. Just reading that there’s a small island off the coast of Italy which is inhabited by 5 million Sicillion people.
That’s the biggest number I’ve ever heard of!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Alison, New Zealand
Friday, December 1, 2023
"If the mean average of 20 gifts is 50 pounds then the total of the 20 gifts will be 20 x 50 = 1000 pound. Assuming that one of the gifts is allowed to be free (0 pounds - is this counted as a whole number of pounds?) then, the cheapest 19 gifts would total the sum of the consecutive whole numbers from 0 to 18. This total can be worked out using the formula (0.5n^2 - 0.5n), or .5 x 19 x 18 = 171 pounds. The most expensive will therefore be 1000 - 171 = 829 pounds.
If the cheapest present is not allowed to be free and is therefore 1 pound, then the cheapest 19 gifts would total the sum of the consecutive whole numbers from 1 to 19. This total can be worked out using the formula (0.5n^2 + 0.5n), or .5 x 19 x 20= 190 pounds. The most expensive will therefore be 1000 - 190 = 810 pounds. "
Allan, Germany
Friday, December 1, 2023
"£810
The 19 cheapest gifts are £1 to £19 then the most expensive is 1000 - sum of 1 to 19. The 1000 is because of 20 x 50.
But you knew all that. "
Søren, Copenhagen
Sunday, December 3, 2023
"The 20 presents cost a total of 20x50= 1000 pounds The cheapest 19 presents cost 19 x 20/2 = 190 pounds. Meaning the most expensive present can cost 1000 - 190= 810 pounds. Hope I did not miss anything. "