
 |
Exam-Style Questions on KinematicsProblems on Kinematics adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher [314] |
Strat drove from Wolverhampton to London via Coventry.
(a) Work out Strat's average speed for his total drive from Wolverhampton to London.
Raven drove from Bedrock to Springfield via South Park.
Raven says that the average speed from Bedrock to Springfield can be found by working out the mean of 70 km/h and 50 km/h.
(b) If Raven is correct, what does this tell you about the two parts of Raven's journey?
2. | GCSE Higher [189] |
The following diagram shows a distance-time graph of the movement of a fish.
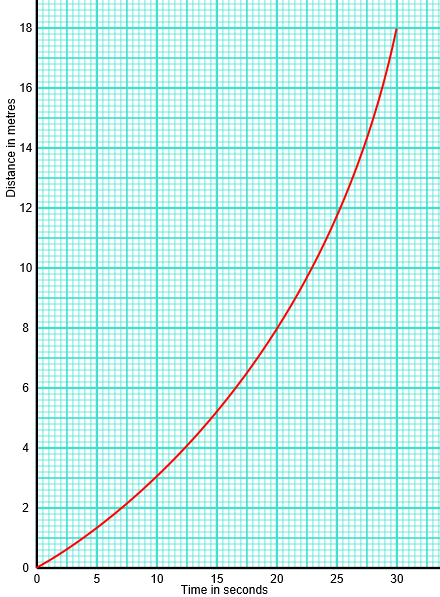
(a) Work out the average speed between 10 and 20 seconds.
(b) Estimate the speed of the fish at 25 seconds.
3. | GCSE Higher [201] |
Marilou and Sam had a skiing race. Here is Marilou’s speed-time graph from the start of the race.
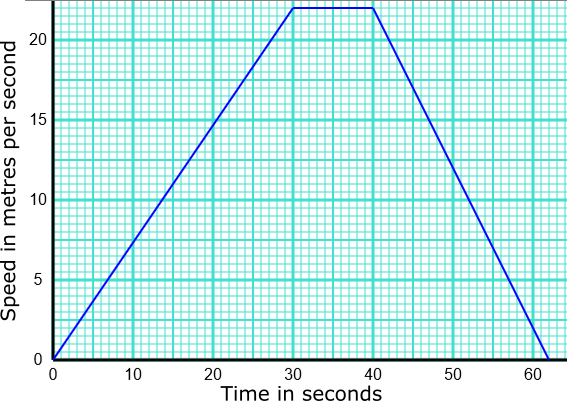
(a) Marilou crossed the finishing line after a time of 40 seconds. How long was the race?
(b) Sam finished after a time of 50 seconds. What was his average speed, in kilometres per hour, for the race?
4. | GCSE Higher [406] |
The distance from Wolverhampton to Cambridge is 115 miles.
Lynn drives from Wolverhampton to Cambridge leaving Wolverhampton at 10:30am. She assumes that her average speed will be 55 mph.
(a) Use Lynn's assumption about her average speed to work out her arrival time in Cambridge.
(b) Lynn's speed was actually lower than her assumption. How does this affect the arrival time?
5. | GCSE Higher [414] |
The following kinematics formula can be used to work out the distance travelled (displacement) of an object travelling with constant acceleration.
$$ s = ut + \frac12 at^2 $$where:
(a) Rearrange the formula to make \(u\) the subject.
(b) What units would be associated with speed in this case?
(c) What units would be associated with acceleration?
6. | GCSE Higher [171] |
A model train is placed on a length of straight track.
(a) Draw a velocity-time graph for the train on graph paper provided below.
(b) Work out the total distance travelled by the model train.
7. | GCSE Higher [522] |
A motorbike moves from rest along a straight road. The graph below shows the speed, \(v\) in metres per second of the motorbike \(t\) seconds after it started to move.
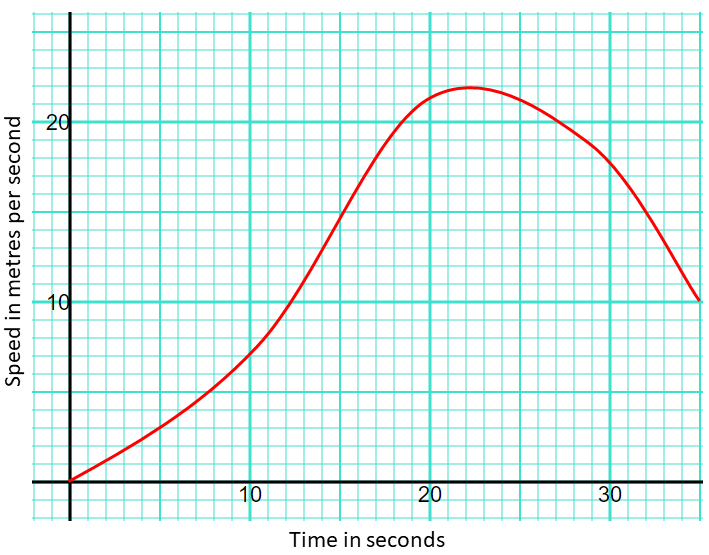
(a) What is the maximum speed achieved by the motorbike.
(b) Calculate an estimate of the gradient of the graph at t = 10.
(c) Describe what your answer to part (b) represents.
(d) Work out an estimate for the distance the motorbike travels in the first 25 seconds of its journey by dividing the area under the graph into five strips of equal width.
8. | GCSE Higher [239] |
Here is a speed-time graph for a go kart.
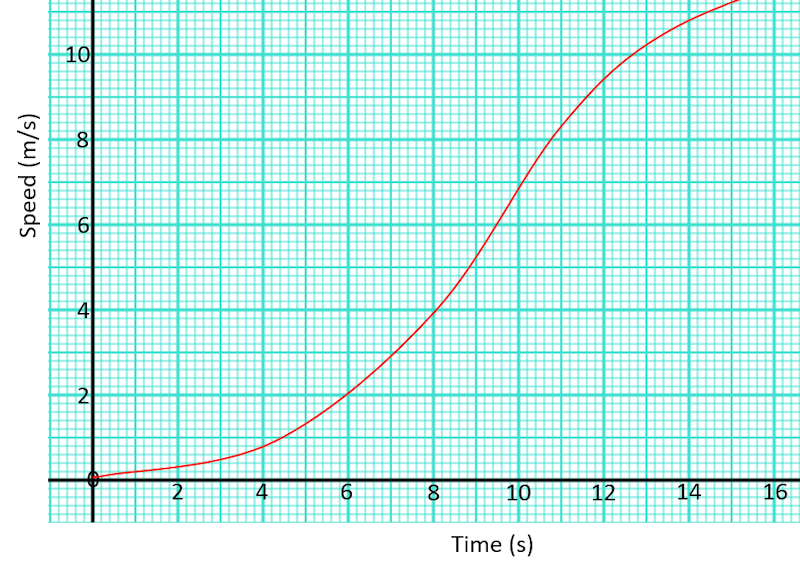
Work out an estimate for the distance the kart travelled in the first 12 seconds by using six strips of equal width.
9. | IB Standard [79] |
Very accurate equipment was used to measure the movement of a particle which moved in a straight line for 3 seconds. Its velocity, \(v\) ms-1 , at time \(t\) seconds, is given by:
$$v=(t^2-5)^3$$(a) Find the velocity of the particle when \(t=2\).
(b) Find the value of t for which the particle is at rest.
(c) Find the total distance the particle travels during the first three seconds.
(d) Show that the acceleration of the particle is given by \(a=6t(t^2-5)^2\)
(e) Find all possible values of t for which the velocity and acceleration are both positive or both negative.
10. | IB Standard [56] |
Pob and Wie are travelling from Bangkok to Khon Kaen.
Pob travels at a velocity given by \(V_P=50-t^2\), where t is in seconds and the velocity is in ms-1.
Wie's displacement from Bangkok in metres is given by \(S_W=2t^2+70\).
When \(t=0\), both vehicles are at the same point.
Find Pob's displacement from Bangkok when \(t=5\).
11. | IB Analysis and Approaches [671] |
A particle moves in a straight line such that its velocity, \(v\) ms-1, at time \(t\) seconds is given by:
$$ v(t)=10e^{-\frac{t}{7}} \sin\left(\frac{t}{2}\right) $$for \( 0 \le t \le 4 \pi\). The graph of \(v\) is shown in the following diagram.
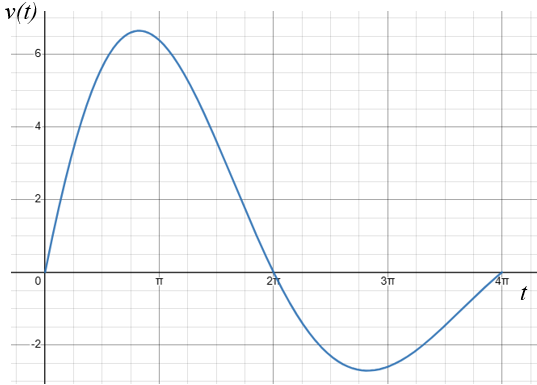
Let \(t_1 \) be the first time when the particle's acceleration is zero.
(a) Find the value of \(t_1\).
(b) Find the distance travelled by the particle between \(t = t_1 \), and t = \(4 \pi \).12. | IB Analysis and Approaches [573] |
A particle travels in a straight line such that its displacement, \(s\) metres, from a fixed point, \(A\), after \(t\) seconds is given by \(s(t) = t^2 - 5t \), for \( 0 \le t \le 10\), as shown in the following sketch.
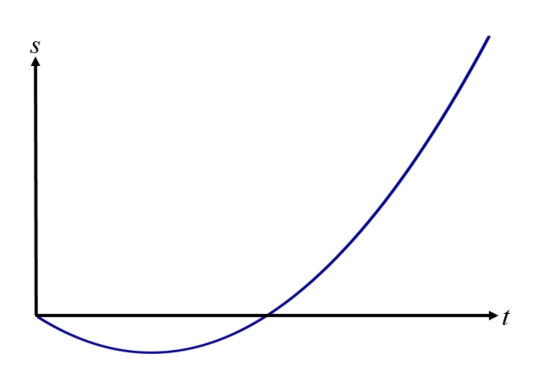
The particle starts at \(A\) and passes through \(A\) again when \(t = q\).
(a) Find the value of \(q\).
The particle changes direction when \(t = r\).
(b) Find the value of \(r\).
(c) Find the displacement of the particle from \(A\) when \(t = r\).
(d) Find distance of the particle from \(A\) when \(t=10\).
(e) Find the total distance travelled by the particle in ten seconds.
A second particle travels along the same straight line such that its velocity is given by \(v(t)=12 - 3t\) for \(t \ge 0\).
When \(t = p\), the distance travelled by this second particle is one metre less than the total distance travelled by the first particle in ten seconds.
(f) Find the value of \(p\)
13. | IB Analysis and Approaches [598] |
A particle P moves along a straight line. The velocity of P is \(v\)ms-l at time \(t\) seconds, where \(v(t) = 5 + 3t - 2t^2\) for \(0 \le t \le 3\). When \(t = 0\), P is at the origin O.
![]() (a) Find the value of \(t\) when P reaches its maximum velocity.
(a) Find the value of \(t\) when P reaches its maximum velocity.
![]() (b) Find the distance of P from O at this time.
(b) Find the distance of P from O at this time.
![]() (c) Sketch a graph of \(v\) against \(t\), clearly showing any points of intersection with the axes.
(c) Sketch a graph of \(v\) against \(t\), clearly showing any points of intersection with the axes.
(d) Find the total distance travelled by P.
14. | IB Analysis and Approaches [616] |
The widest river in the world has a width of 11km at its widest point. Suppose there were a straight length of this river near Awkwardville (A) as shown in the diagram below. Points A and P lie on opposite banks, such that AP is the shortest distance across the river. Point B represents the centre of Bumblingburg which is located on the southern riverbank.
$$PB = 40km, AP = 11km \text{ and angle } A \hat{P}B = 90° $$A boat travels at an average speed of \(12km h^{-1}\).
A bus travels along the straight road
between P and B at an average speed of \(30kmh^{-1}\).
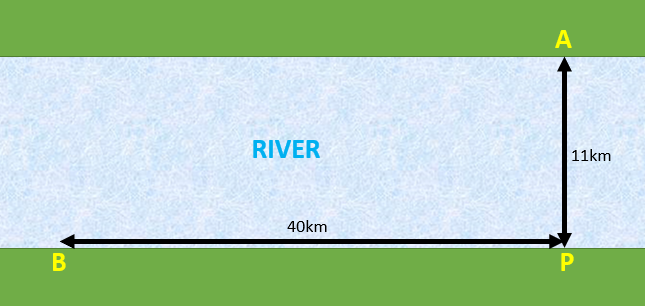
(a) Find the travel time, in hours, from A to B given that the boat is taken from A to P, and the bus from P to B.
(b) Find the travel time, in hours, from A to B given the boat travels directly to B.
There is a point D which lies on the road from P to B. such that \(BD = x km\).
(c) If the boat travels from A to D and the bus travels from D to B, find an expression, in terms of \(x\), for the travel time T, from A to B, passing through D.
(d) Find the value of \(x\) so that T is a minimum.
An excursion involves renting the boat and the bus. The cost to rent the boat is £50 per hour and the cost to rent the bus is £35 per hour.
(e) Find the new value of \(x\) so that the total cost to travel from A to B via D is a minimum.
(f) Write down the minimum total cost for this journey.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.