
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
Lyana has drawn a time series graph to show the number of minutes she spent doing homework on some of the days in June 2021.
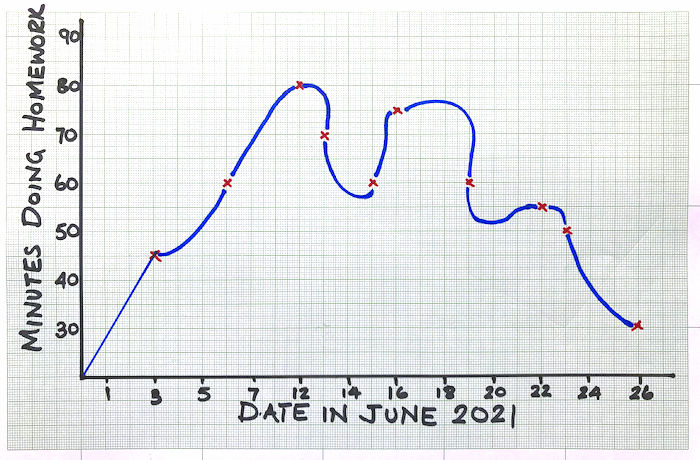
Write down two things that are wrong or could be misleading with this graph.
2. | GCSE Higher |
The following diagram shows a distance-time graph of the movement of a fish.
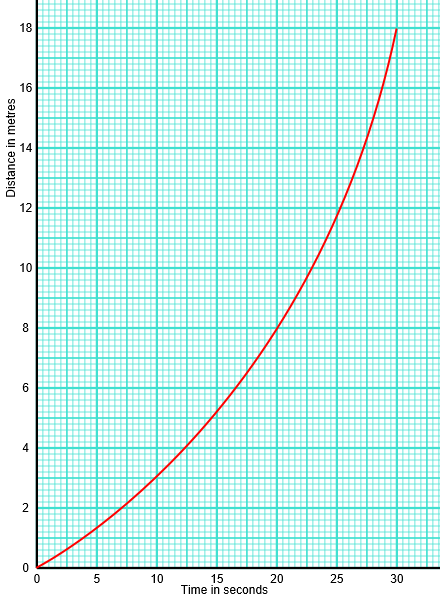
(a) Work out the average speed between 10 and 20 seconds.
(b) Estimate the speed of the fish at 25 seconds.
3. | GCSE Higher |
Marilou and Sam had a skiing race. Here is Marilou’s speed-time graph from the start of the race.
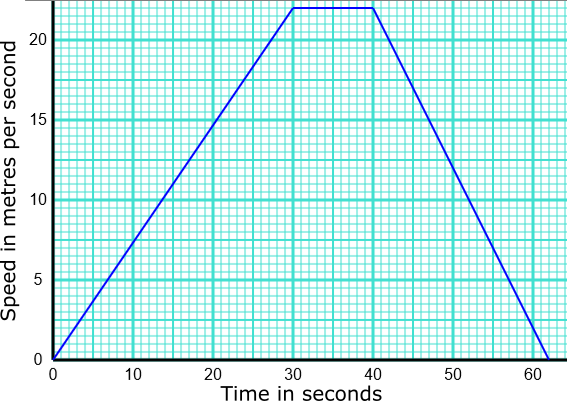
(a) Marilou crossed the finishing line after a time of 40 seconds. How long was the race?
(b) Sam finished after a time of 50 seconds. What was his average speed, in kilometres per hour, for the race?
4. | GCSE Higher |
A model train is placed on a length of straight track.
(a) Draw a velocity-time graph for the train on graph paper provided below.
(b) Work out the total distance travelled by the model train.
5. | GCSE Higher |
Here is a speed-time graph for a go kart.
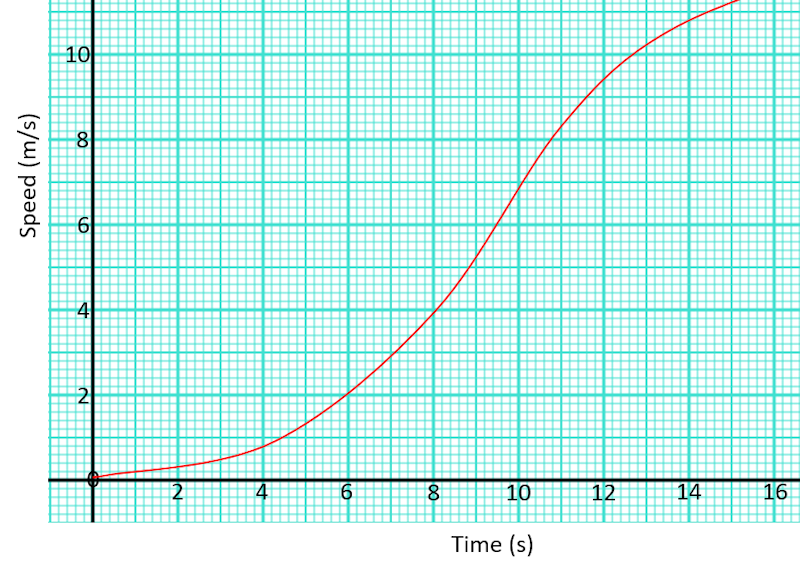
Work out an estimate for the distance the kart travelled in the first 12 seconds by using six strips of equal width.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.