

Drag the green circles above to design your snowflake.

InstructionsTry your best to answer the questions above. Type your answers into the boxes provided leaving no spaces. As you work through the exercise regularly click the "check" button. If you have any wrong answers, do your best to do corrections but if there is anything you don't understand, please ask your teacher for help. When you have got all of the questions correct you may want to print out this page and paste it into your exercise book. If you keep your work in an ePortfolio you could take a screen shot of your answers and paste that into your Maths file. |
||
|
|
||
|
|

|
More Activities: |
|
Mathematicians are not the people who find Maths easy; they are the people who enjoy how mystifying, puzzling and hard it is. Are you a mathematician? Comment recorded on the 10 September 'Starter of the Day' page by Carol, Sheffield PArk Academy: "3 NQTs in the department, I'm new subject leader in this new academy - Starters R Great!! Lovely resource for stimulating learning and getting eveyone off to a good start. Thank you!!" Comment recorded on the 6 May 'Starter of the Day' page by Natalie, London: "I am thankful for providing such wonderful starters. They are of immence help and the students enjoy them very much. These starters have saved my time and have made my lessons enjoyable." |
Each month a newsletter is published containing details of the new additions to the Transum website and a new puzzle of the month. The newsletter is then duplicated as a podcast which is available on the major delivery networks. You can listen to the podcast while you are commuting, exercising or relaxing. Transum breaking news is available on Twitter @Transum and if that's not enough there is also a Transum Facebook page. |
|
AnswersThere are answers to this exercise but they are available in this space to teachers, tutors and parents who have logged in to their Transum subscription on this computer. A Transum subscription unlocks the answers to the online exercises, quizzes and puzzles. It also provides the teacher with access to quality external links on each of the Transum Topic pages and the facility to add to the collection themselves. Subscribers can manage class lists, lesson plans and assessment data in the Class Admin application and have access to reports of the Transum Trophies earned by class members. If you would like to enjoy ad-free access to the thousands of Transum resources, receive our monthly newsletter, unlock the printable worksheets and see our Maths Lesson Finishers then sign up for a subscription now: Subscribe |
||
Go MathsLearning and understanding Mathematics, at every level, requires learner engagement. Mathematics is not a spectator sport. Sometimes traditional teaching fails to actively involve students. One way to address the problem is through the use of interactive activities and this web site provides many of those. The Go Maths page is an alphabetical list of free activities designed for students in Secondary/High school. Maths MapAre you looking for something specific? An exercise to supplement the topic you are studying at school at the moment perhaps. Navigate using our Maths Map to find exercises, puzzles and Maths lesson starters grouped by topic. | ||
Teachers | ||
|
If you found this activity useful don't forget to record it in your scheme of work or learning management system. The short URL, ready to be copied and pasted, is as follows: |
Alternatively, if you use Google Classroom, all you have to do is click on the green icon below in order to add this activity to one of your classes. |
It may be worth remembering that if Transum.org should go offline for whatever reason, there is a mirror site at Transum.info that contains most of the resources that are available here on Transum.org. When planning to use technology in your lesson always have a plan B! |
|
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments. |
||
© Transum Mathematics 1997-2025
Scan the QR code below to visit the online version of this activity.
https://www.Transum.org/go/?Num=886
Transum with help from Wikepedia,
Tuesday, December 8, 2020
"There is a limit to how snowflake-like your creations can be with this application as it was designed to focus primarily on the notion of symmetry. In real life snowflakes are never completely symmetrical but do commonly have rotational symmetry of order 6 in addition to six lines of symmetry. The symmetry is due to the hexagonal crystalline structure of ice. Beginning with a tiny hexagon the six "arms" of the snowflake then grow independently from each of the corners of the hexagon. The microenvironment in which the snowflake grows changes dynamically as the snowflake falls through the clouds and tiny changes in temperature and humidity affect the way in which water molecules attach to the snowflake. Since the micro-environment (and its changes) are very nearly identical around the snowflake, each arm tends to grow in nearly the same way."
Transum,
Wednesday, December 9, 2020
"Display idea: Print then cut out your snowflake designs as part of your classroom Christmas decorations. They can be made all the more colourful if two or more snowflakes are designed then one pasted on top of the other in your paint program.
 ."
."
Cosette, Timmel
Tuesday, December 15, 2020
" "
"
LeAnne, Virginia
Wednesday, December 23, 2020
" "
"
Tangerang, Indonesia
Thursday, February 11, 2021
" "
"
EJ, TGS
Thursday, February 11, 2021
" "
"
EJ, TGS
Thursday, February 11, 2021
" "
"
Adam Moore,
Tuesday, May 25, 2021
" "
"
Glenda, New Zealand
Tuesday, October 26, 2021
" "
"
S. Knowman, Lapland
Tuesday, October 26, 2021
" "
"
Gamosa, Bandar Seri Begawan
Sunday, February 20, 2022
" "
"
Chickienuggiexox, Somerset
Thursday, March 17, 2022
" "
"
Chickienuggiexox, Somerset
Thursday, March 17, 2022
"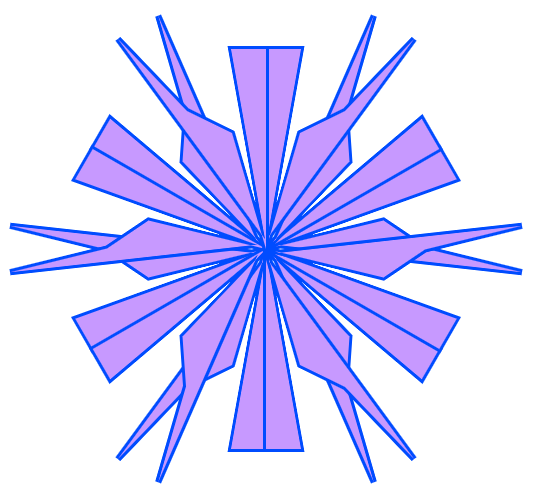 "
"
Chickienuggiexox, Somerset
Thursday, March 17, 2022
" "
"
Chickienuggiexox, Somerset
Thursday, March 17, 2022
" "
"
Dan, US
Wednesday, July 13, 2022
" "
"
Darcie, Perth
Wednesday, November 23, 2022
" "
"
Lesley, Silver Spring
Monday, December 5, 2022
" "
"
Joe, Christchurch
Thursday, December 8, 2022
" "
"
Huzaifa, Australie
Thursday, December 8, 2022
"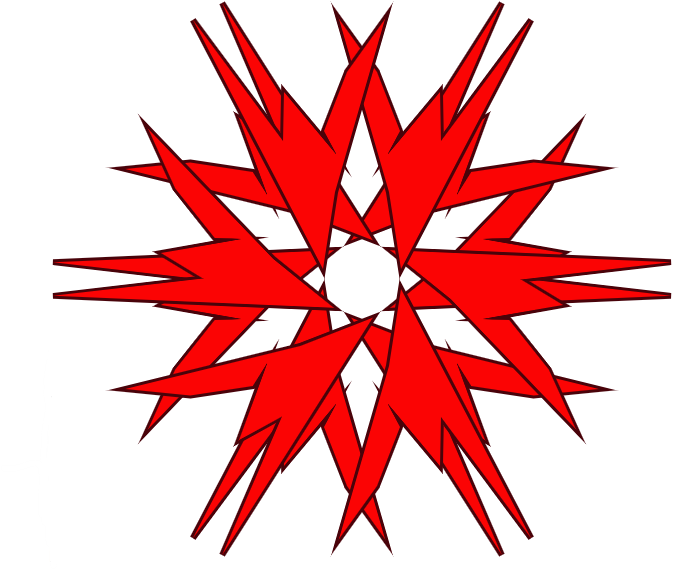 "
"
JenJun, Salt Lake City
Monday, January 16, 2023
"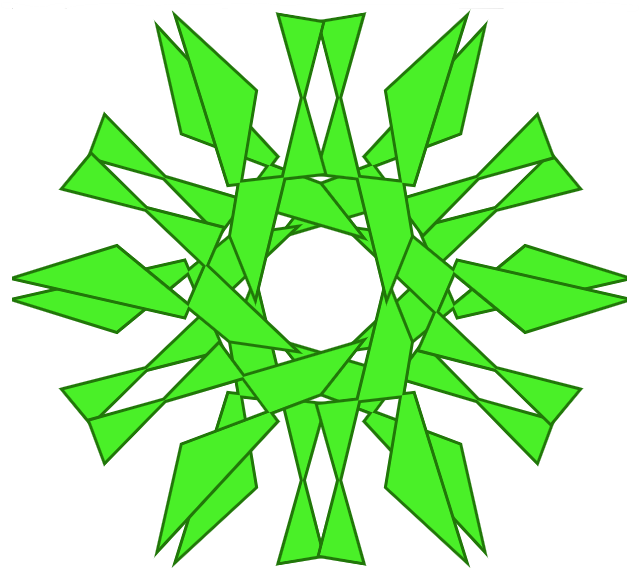 "
"
Corrie, Texas
Monday, April 17, 2023
"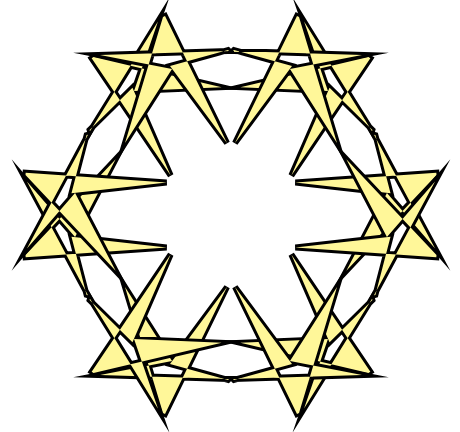 "
"
W Hartwell White, Albuquerque
Monday, December 11, 2023
" "
"
Sun Clouds,
Thursday, December 14, 2023
" "
"
Ethan,
Thursday, December 14, 2023
" "
"
William,
Thursday, December 14, 2023
" "
"
Sasha, Maine
Thursday, December 21, 2023
" "
"
Enojon, Mexico
Thursday, January 4, 2024
" "
"
Josie, Vermont
Monday, January 22, 2024
" "
"