Cookies are used on this website.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

• Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run.
• Straight Line Graphs Video After drawing a straight line graph learn about its equation in the form y = mx + c.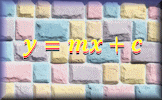
• Straight Line Graph Equation An online exercise about the equation y=mx+c and the features of a straight line graph.
• Don's Graph Snaps Complete the tables and find the equations of the graphs that can be seen in the snaps.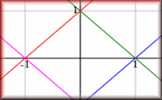
• Graph Patterns Find the equations which will produce the given patterns of graphs.
• Straight Line Graphs 10 straight line graph challenges for use with computer graph plotting software or a graphical display calculator.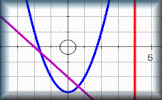
• Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
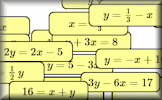• Parallel Graphs Collect together in groups the equations of the graphs that are parallel to each other.
• Perpendicular Pairs Find the pairs of equations that will produce perpendicular graphs.
• Equation of Line through Points Video A short video showing how to find the equation of a line that passes through given points.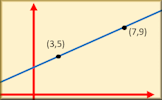
• Equation of a Line Through Points Match the equations of the straight line graphs to the clues about gradients and points.
• Coordinate Geometry Table Fill in the empty cells of this table with information about lines, gradients and coordinates.

Here are some exam-style questions on this statement:

• "The equation of the line L₁ is $y = 2 - 5x$." ... more
• "Which of the following lines is parallel to the x-axis?" ... more
• "Show that line $5y = 7x - 7$ is perpendicular to line $7y = -5x + 55$." ... more
• "A straight line goes through the points $(a, b)$ and $(c, d)$, where" ... more
• "The straight line $L$ has the equation $4y = 3x + 5$." ... more
• "A is the point (-5, -9) and B is the point (10, 1)." ... more
• "Suppose a rhombus ABCD is drawn on a coordinate plane with the point A situated at (4,7). The diagonal BD lies on the line $y = 2x - 5$" ... more
• "Consider the points A(-5, 15). B(4, 6) and C(-8, 12). The line $L$ passes through the point A and is perpendicular to [BC]." ... more
• "Consider a straight line graph L1, which intersects the x-axis at A(8, 0) and the y-axis at B (0, 4)." ... more
• "The vertices of quadrilateral ABCD are A (2, 4), B (-1, 5), C (–3, 4) and D (–2, 2)." ... more

See all these questions

Here is an Advanced Starter on this statement:

• Parallel Graphs
  Determine from their equations which of the straight line graphs are parallel and perpendicular. more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.