Geometry Starters:
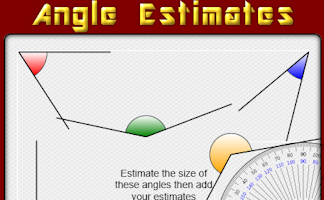
Estimate the sizes of each of the angles then add your estimates together.

How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?

Which of the two shapes has the largest area? You will be surprised!
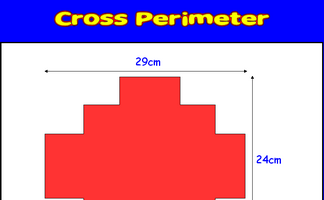
Calculate the distance around the given shape

A dice is reflected in two mirrors. What numbers can be seen?

On a full page in the back of your exercise book draw a perfectly regular hexagon.
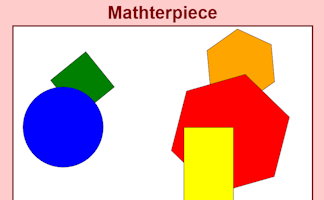
Memorise a picture made up of geometrical shapes

Find the dimensions of a rectangle given the perimeter and area.

On a full page in the back of your exercise book draw a perfectly regular pentagon.

Solve the riddle to find the name of the polygon then sum the interior angles.

Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
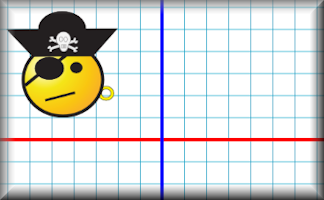
On squared paper copy the drawing of the face then reflect it in three different lines.

Draw a pattern with rotational symmetry of order 6 but no line symmetry.

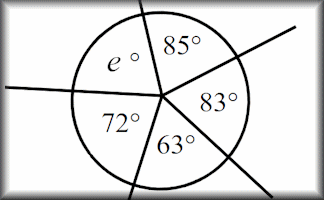
Work out which sectors fit together to make complete circles. Knowledge of the sum of the angles at a point will help find more than one correct solution to this puzzle.
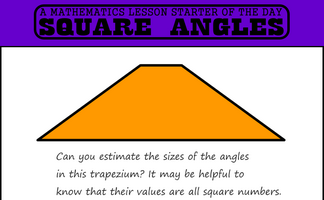
Find a trapezium, a triangle and a quadrilateral where all of the angles are square numbers.

Write down the names of all the mathematical shapes you know.
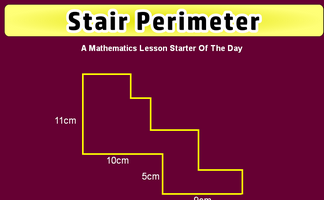
Use the information implied in the diagram to calculate the perimeter of this shape.

Is it possible to work out the perimeter of this shape if not all the side lengths are given?
Exercises
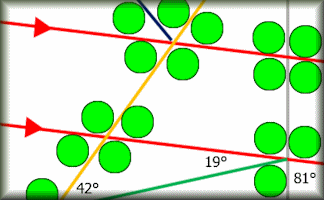
Angle Chase
Find all of the angles on the geometrical diagrams.
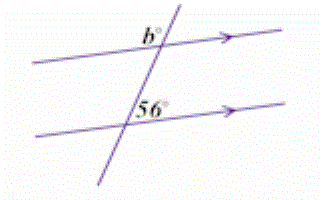
Angle Parallels
Understand and use the relationship between parallel lines and alternate and corresponding angles.
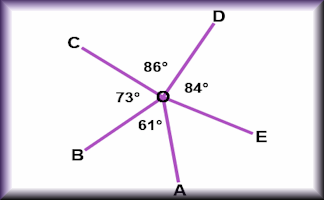
Angle Points
Apply the properties of angles at a point, angles on a straight line and vertically opposite angles.
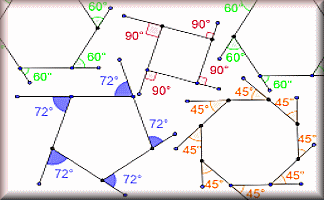
Angle Theorems
Diagrams of the angle theorems with interactive examples.
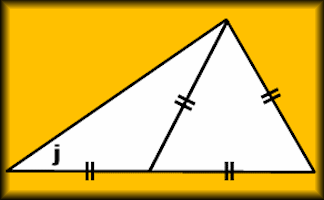
Angles in a Triangle
A self marking exercise involving calculating the unknown angle in a triangle.
Angles Mixed
Find the unknown angles by using the basic angle theorems.
Area Maze
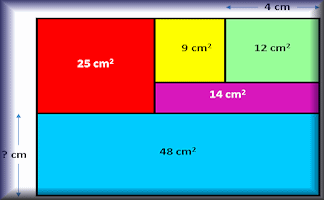
Use your knowledge of rectangle areas to calculate the missing measurement of these composite diagrams.
Area of a Triangle
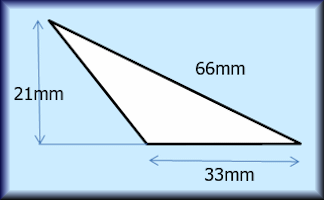
Calculate the areas of the given triangles in this self marking quiz.
Area Two
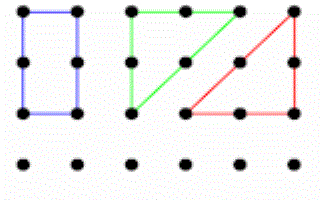
How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
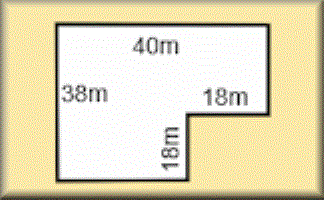
Areas of Composite Shapes
Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.

Circle Parts Kim's Game
A memory game to be projected to help the whole class revise the names for the parts of a circle.
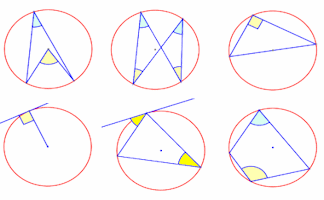
Circle Theorems
Diagrams of the circle theorems to be projected onto a white board as an effective visual aid.
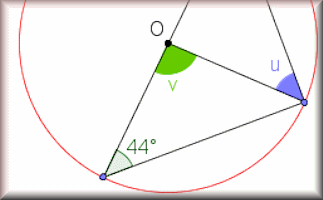
Circle Theorems Exercise
Show that you understand and can apply the circle theorems with this self marking exercise.
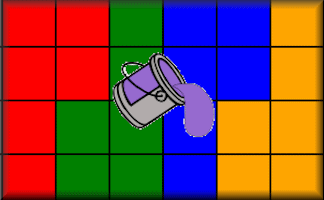
Congruent Parts
Use the colours to dissect the outlines into congruent parts.

Congruent Triangles
Test your understanding of the criteria for congruence of triangles with this self-marking quiz.

Estimating Angles
Estimate the size of the given acute angles in degrees.
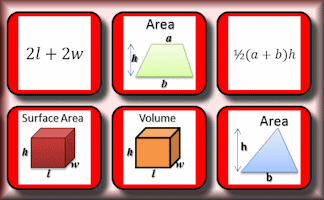
Formulae Pairs
Find the matching pairs of diagrams and formulae for basic geometrical shapes.
Geometry Toolbox
Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.

Kite Maths
Can you make a kite shape from a single A4 size sheet of paper using only three folds?

Measuring Units
Check your knowledge of the units used for measuring with this self-marking quiz about metric and imperial units.
Pin Board
Rows and columns of dots that can be joined using straight lines to create shapes.

Polybragging
The Transum version of the Top Trumps game played online with the properties of polygons.

Polygon Angle Explorer
Barbara Bug walks around a regular hexagon turning through each of the exterior angles as she goes.
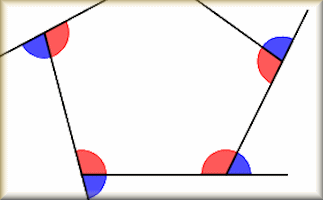
Polygon Angles
A mixture of problems related to calculating the interior and exterior angles of polygons.
Polygon Pieces
Arrange the nine pieces of the puzzle on the grid to make different polygons.

Polygon Profiles
A visual aid about the properties of regular polygons designed to be projected onto a whiteboard for whole class exposition.

Polygon Properties
Connect the names of the polygons with the descriptions of their properties.
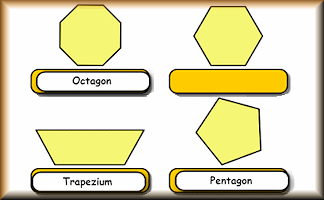
Polygons
Name the polygons and show the number of lines and order of rotational symmetry.
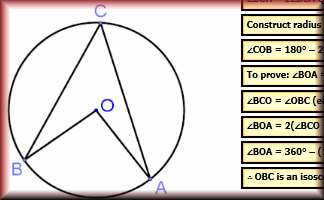
Proof of Circle Theorems
Arrange the stages of the proofs for the standard circle theorems in the correct order.
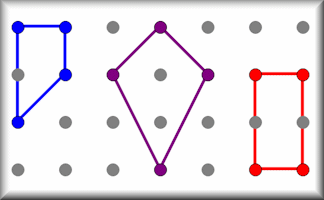
Quad Areas
Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.

Similar Parts
Use the colours to dissect the outlines into similar parts.
Surface Area
Work out the surface areas of common solid shapes in this collection of exercises.
Transformations
Draw transformations online and have them instantly checked. Includes reflections, translations, rotations and enlargements.
Volume
Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Words and Concepts
Fill in the missing words to show an understanding of the vocabulary of equations, inequalities, angles and shapes.
Other activities for this topic | | |
Complete Index of Starters