Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Time for some detective work!
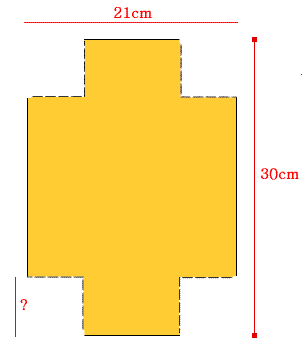
A tray is to be made from a special sheet of paper which is 30cm by 21cm.
Squares will be cut from each of the corners of the paper and the edges folded up to form the tray.
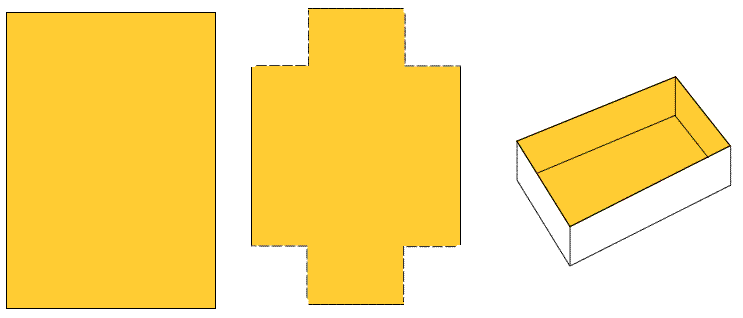
What should be the size of the cut out squares if the tray is to have the largest possible volume?
Use algebra, let the side of the cut out square be x.
Use some scrap A4 paper to try out your ideas.
Use a spreadsheet to record your working.
Discuss your thoughts with someone else.
Draw a graph of your results.
Work systematically.
Did you find the maximum volume of the tray?
You can claim a Transum virtual trophy if you got the correct answers:
| Length of sides of cut-out squares: | cm to three significant figures. |
| Maximum volume of tray: | cm3 to three significant figures. |
Note that you do not have to get the answer right to prove you have done a good investigation. Your teacher is the best person to give you feedback on your work.
The solutions to this and other Transum puzzles, exercises and activities are available here when you are signed in to your Transum subscription account. If you do not yet have an account and you are a teacher, tutor or parent you can apply for one by completing the form on the Sign Up page.
A Transum subscription also gives you access to the 'Class Admin' student management system, downloadable worksheets, many more teaching resources and opens up ad-free access to the Transum website for you and your pupils.
Extend your investigation to include sheets of paper of different sizes.
What if the tray needed a lid?
Think about the surface area, the minimum volume or other shape trays.
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
A mathematical investigation is quite different to other mathematical activities. The best investigations are open ended and allow students to choose the way they work and how they record their findings. It is one of the few occasions when 'going off on a tangent' is not only acceptable but actively encouraged (within reason).
Students may ask for 'the answers' but this supposes that the activity is
closed. Investigations can always be extended by varying the initial
instructions or asking the question 'what if...?'. Sometimes students point out
that the instructions are ambiguous and can be interpreted in different ways.
This is fine and the students are encouraged to explain how they interpreted the
instructions in their report.
Some students may benefit from a writing frame when producing the reports
of their investigations. Teachers may suggest sections or headings such as
Introduction, Interpretation, Research, Working and Conclusion or something
similar.
Featured ActivityWhere's Wallaby? Find the hidden wallaby using the clues revealed at the chosen coordinates. Not only is this a fun way to practise using coordinates it is also a great introduction to Pythagoras' theorem and loci. |
SuggestedRemainder Race A game involving chance and choice requiring an ability to calculate the remainder when a two digit number is divided by a single digit number. |
Recently UpdatedShape Sorter Drag each shape into the correct bin according to their types and symmetries. So far this activity has been accessed 198 times and 96 Transum Trophies have been awarded for completing it. |
