Areas Investigation
Investigate polygons with an area of 4 sq. units.
 |
|
|
|
|
|
 |
 |
|
|
|
|
|
|
|
|
Use printable square spotty paper and a pencil for an alternative method of constructing the polygons.
SuggestedHow Many Squares? 2
A printable grid containing many copies of the design used in the second
shape counting Starter. |
RelatedAreas of Composite Shapes
Find the areas of combined (composite) shapes made up of one or more simple
polygons and circles. |
Similar ActivityPolygon Hunting
Find all the polygons that can be drawn by joining dots on this seven dot grid. |
Teacher notes for this and solutions to other Transum puzzles, exercises and activities are available here when you are signed in to your Transum subscription account. If you do not yet have an account and you are a teacher, tutor or parent you can apply for one by completing the form on the Sign Up page.
A Transum subscription also gives you access to the 'Class Admin' student management system, downloadable worksheets, many more teaching resources and opens up ad-free access to the Transum website for you and your pupils.
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
A mathematical investigation is quite different to other mathematical activities. The best investigations are open ended and allow students to choose the way they work and how they record their findings. It is one of the few occasions when 'going off on a tangent' is not only acceptable but actively encouraged (within reason).
Students may ask for 'the answers' but this supposes that the activity is
closed. Investigations can always be extended by varying the initial
instructions or asking the question 'what if...?'. Sometimes students point out
that the instructions are ambiguous and can be interpreted in different ways.
This is fine and the students are encouraged to explain how they interpreted the
instructions in their report.
Some students may benefit from a writing frame when producing the reports
of their investigations. Teachers may suggest sections or headings such as
Introduction, Interpretation, Research, Working and Conclusion or something
similar.
Featured ActivityNine Digits Arrange the given digits one to nine to make three numbers such that two of them add up to the third. This is a great puzzle for practicing standard pen and paper methods of three digit number addition and subtraction. |
Recently UpdatedCoins and Notes Sharpen your money management skills by accurately calculating sums and working out change. So far this activity has been accessed 224 times and 23 Transum Trophies have been awarded for completing it. |
Transum,
Tuesday, March 3, 2015
"The Areas Investigation grid above could be used to play a game. Two players take it in turns to draw a shape with an area of four. If a player is unable to think of a shape that hasn't been drawn before, then the other player wins. No reflections or rotations of shapes already drawn are allowed."
Will Emeny,
Thursday, September 8, 2016
"The following puzzle comes from the excellent Mr Barton's podcasts and was suggested by Will Emeny.
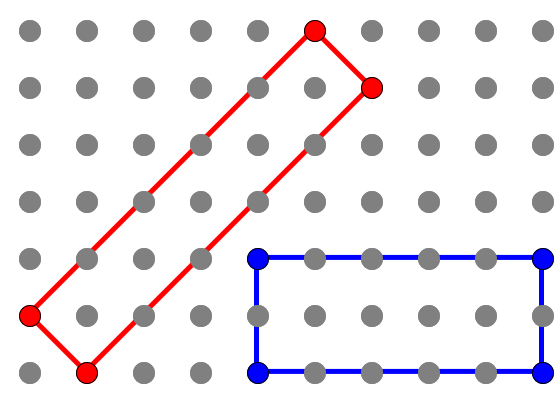
These two rectangles have an area of 10 square units.
In total, there are five different rectangles with vertices on grid points that have an area of 10 square units. Draw all five.
Prove there can be no more than five.
Draw all the rectangles that have an area of 12 square units. How do you know you've got them all?"