
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
The diagram shows two triangles, ABD and BCD.
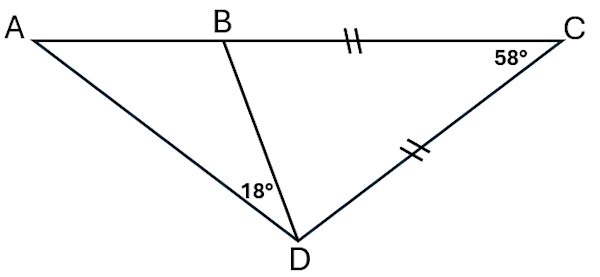
ABC is a straight line, CB = CD, angle ADB = 18° and angle BCD = 58°.
Work out angle DAB.
2. | GCSE Higher |
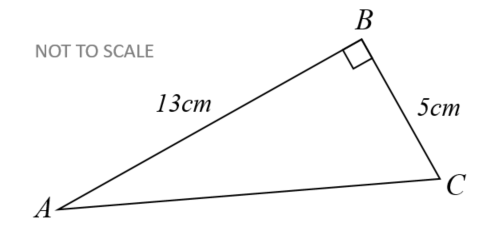
\(ABC\) is a right-angled triangle.
John has a method for finding the length of \(AC\)
 $$AC^2 = AB^2 - BC^2$$
$$AC^2 = 13^2 - 5^2$$
$$AC^2 = 169 - 25$$
$$AC^2 = 144$$
$$AC = \sqrt{144}$$
$$AC = 12$$
$$AC^2 = AB^2 - BC^2$$
$$AC^2 = 13^2 - 5^2$$
$$AC^2 = 169 - 25$$
$$AC^2 = 144$$
$$AC = \sqrt{144}$$
$$AC = 12$$
John's answer of \(12cm\) is not correct.
(a) What mistake has he made with his method?
(b) Show the correct method and the correct answer to 3 significant figures.
3. | GCSE Higher |
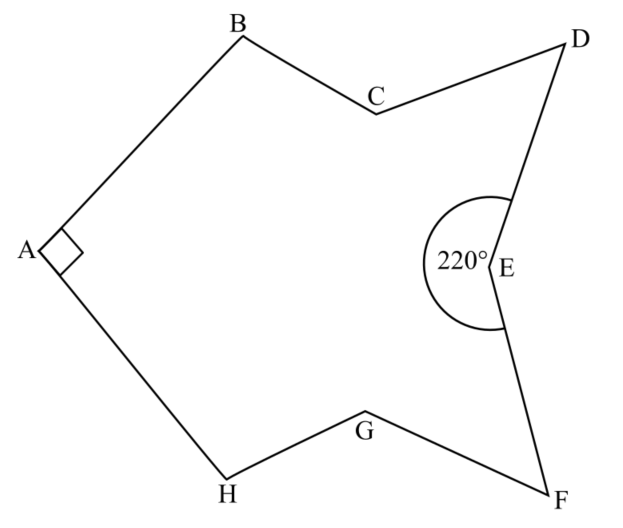
The diagram, not drawn to scale, show a polygon with one line of symmetry, AE.
Angle HAB is 90° and interior angle DEF is 220°.
Work out the size of angle ABC which is half the size of interior angle BCD and twice the size of angle CDE.
4. | GCSE Higher |
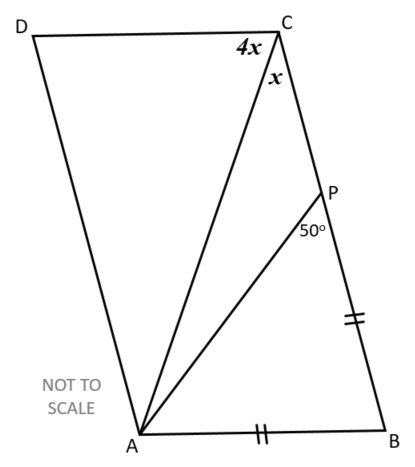
A point P is marked on side BC of parallelogram ABCD such that AB = BP.
Find the value of angle \(x\).
5. | GCSE Higher |
The diagram shows a quadrilateral ABCD in which angle DAB equals angle CDA and AB = CD.

Prove that the diagonals of this quadrilateral are of equal length.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.