

The effect is that the class all contribute to the free selection of a number which the teacher had predicted in advance.
To set up this trick you need to firstly choose the target number and write this down as your "prediction"! This should be done before the class have arrived for their lesson. Your prediction can be sealed in an envelope or, for more of a showy reveal, written on the back of a picture hanging in the room.
For the purposes of this explanation the target number is 36.9. Easy for you to remember as it is normal human body temperature (you knew that didn't you)?
So the trick begins with you asking a student at random to choose a number between 1 and 100 which you have written on the board like this:
If the student offers a number which is larger than the target number you replace the bottom number with the student's number, otherwise you replace the top number.
Let's imagine the student offers the number 40. Your board should now look like this:
The next number you ask for has to be between 1 and 40 (the new top and bottom numbers).
Let's imagine the next five students you pick at random offer the numbers 20, 30, 35, 37.5 and 36.5. Your board should now look like this:
Can you see how by deciding to put the students' numbers in either the top or bottom rows you are zooming in on the target number? Eventually one of the students will offer the target number. You then white it in large digits spanning both rows. You say something like "I think that's enough to ensure many of you have contributed to selecting the class' chosen number". You then reveal your prediction and all are amazed!
Liam Delap is an English professional footballer who plays as a striker for Premier League club Chelsea. His other claim to fame is that he can quickly calculate the cube roots of large numbers in his head!

Show friends and family your amazing mental mathematical skills with huge numbers using these Cube Root Instructions.
This trick works best on the standard iPhone calculator* though other calculators may have the same way of working and could also be used.
The effect is that pupils come up with random two and three digit numbers which you multiply together. Irrespective of what numbers they come up with the product will be the same as the number you had previously predicted.
To set up the trick you need to have previously chosen the large number as your prediction. This should be done before the class have arrived for their lesson. Your prediction can be sealed in an envelope or, for more of a showy reveal, written on the back of a picture hanging in the room.
The other essential part of the setup is to type your predicted number into the calculator then press the plus button, the zero button and the multiplication button … nothing else.
When the students call out their random two and three digit numbers you type them into the calculator pressing the multiplication button between each one. This should be done in full view of the students so that can see that you are not doing anything sneaky! After five or six numbers you press the equals sign and, as if by magic, the predicted number appears on the calculator screen. You then reveal your prediction and all are amazed!
How does it work? Well it involves the principle of the Order of Operations or BIDMAS. Let's imagine the students' numbers were 19, 345, 21, 999 and 456 and your prediction was 1,601,863.
The numbers entered into the calculator were:
1601863 + 0 x 19 x 345 x 21 x 999 x 456
The students didn't see the first two numbers entered as you did this before they arrived. The calculator performs the multiplications before the addition so the product of zero is added to your prediction. Magic!
*Sadly recent iOS updates (18+) prevent this trick working as describod.
The effect is that you can add up ten numbers in your head faster than anyone in the class can do it with a calculator.
A volunteer from the class is chosen to be the calculator operator. Another student, with good handwriting, is chosen as the Scribe, to write on the board.
You, the teacher, and the calculator operator stand with your backs to the board so you can't see the numbers being written.
The scribe is told to write down a one digit number then, underneath that, to write a second one digit number.
A third number, the sum of the first and second numbers, should now be written down.
A fourth number, the sum of the second and third numbers, should also be written down.
The scribe continues to write down numbers, each one being the sum of the previous two, until there are ten numbers in the list altogether.
At this point you and the calculator operator turn to face the board in a race to find the total.
The trick is that rather than attempt to add all of the numbers together you simply multiply the seventh number by 11. It will give you the total that will take the calculator operator more time to work out. The class will be amazed at your numeracy skills!
How does it work? There are two tricks involved. The first is the quick way of multiplying by eleven and the other is related to the fact that this is a Fibonacci type sequence.
Let the first and second numbers selected be x and y respectively. The ten terms of the sequence will be x, y, x+y, x+2y, 2x+3y, 3x+5y, 5x+8y, 8x+13y, 13x+21y and 21x+34y.
The sum of this sequence is 55x + 88y which is 11 times 5x+8y.

This trick appears to be mathematical but perhaps it is not!
Can you change this square into two using only a pencil? You are not allowed to come anywhere near the screen (or whiteboard).

The Trick: Carefully use the blunt end of a pencil to push up the lower eye lid of one eye and you will see double!
Each student is asked to think of a number between 2 and 9 inclusive (or ace, jack, queen or king). Whatever number they have chosen, there are four cards in their pack with that value. Students are asked to shuffle the pack while thinking about their cards.
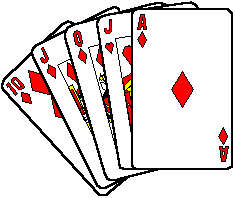
Students are considered to have magical powers if two of their cards come
together in the pack (well there might be one card between them but for the
purposes of this exercise we will call that coming together).
Most students should find that this works for them ... so they have magic
powers ... or have they?
The Trick: In fact this is an example where the odds are weighted in
favour of a success ... can you estimate the probability from the results of
this activity?
"There aren't many grey elephants living in Denmark are there?"
Virtually everyone in the room will have thought of Denmark as their country
and as elephant as their animal. Is this magic?
Students can now investigate the probability of this happening. Having first
satisfied themselves that everyone will arrive at the letter D independently
of their starting number, how many countries are there starting with D?
How many animals beginning with E? Of all the animals beginning with E how
likely is a person to choose elephant? Perhaps a survey might answer this
question.
Students could now be asked to make up for themselves a similar trick (but
not using Elephants from Denmark). Try out the tricks on some other students
and teachers.
Finally a demonstration of tree diagrams can be used to explain the
probabilities of these tricks working.

Update November 2014: The 96% and 85% on the tree diagram above were made-up figures for illustrative purposes only. We have now conducted our own survey to see what those figures should be. You can see the results on the Predictive Survey Results page.]
You can amaze your students by pretending to add up a whole column of
three digit numbers in a couple of seconds.
Ask three students to write three digits each on a piece of paper as if they
are to be added and return the paper to you.
You write two more numbers below those. Choose your first number (which is
the fourth one in the problem) so that the first number and fourth numbers
add up to 999. Choose your next number so that it adds with the second
number to give 999.
283
234
549
716
765
Give a student the paper and ask them to add up the numbers on a
calculator. Then the student could return the paper to you. Look at it
briefly as if you are adding the numbers in your head and announce the
answer.
The answer will be 2000 plus the third number minus 2 which you could
compute very quickly once the student returns the paper.
This could be followed by a class discussion about how this trick works ...
students practise with friends.
The Teacher writes a number on a large piece of paper. The students can
see this going on but can't see which number it is. The paper is the put in
an envelope or a box and put in a safe place in view of the students.
The Teacher then asks a student to think of a very large number. This number
is written on the board in words.
"How many letters are in these words?" ... the answer is written underneath
in words...."How many letters are in these words?" ... and so on repeating
the process again and again till the list of numbers has reached the bottom
of the board. The envelope is then opened to reveal the number FOUR which
will be the last number written on the board.
F O U R
"What if we start with a different number?" ... another student
volunteers a different starting number which eventually generates four
again.
"Does this always happen?".. students try some of their own.
"Why does it always happen?"
"What about other languages?"
Students now do an investigation looking at the properties of the number
words in different languages. They can use foreign language dictionaries or
the internet as appropriate. They should produce a write up of their
findings for their folders.
many calculations have short cuts or tricks associated with them which enable students to perform the calculations quickly in their heads.
Here are a couple of examples:
Quick Square
Did you know that there is a quick way of squaring a two digit number
which ends in 5?
Just multiply the first digit by that number plus one.... stick a 25
after your product and there's your answer .... simple ?
Example:
Q. What is 35 squared?
A. 3x4=12
.....now stick on the 25
...........the answer is 1225
Do you know why it works?
Times Eleven
The eleven times table has always been very easy to learn up to 9 x 11.
Here's a way of multiplying large numbers by 11 too:
Example:
Q. What is 324 x 11 ?
A. Write down the first digit ... 3
.......Add the first and second digits ... 3 + 2 = 5
.......Add the second and third digits .. 2 + 4 = 6
.......Write down the last digit ........... 4
The answer is 3564.
Try it yourself ... multiply 543 by 11
Do you know why it works?
Does it work for all three digit numbers?
A large house plan made from 9 pieces of carpet (each 3m by 3m) is set out in the middle of a large room as shown:
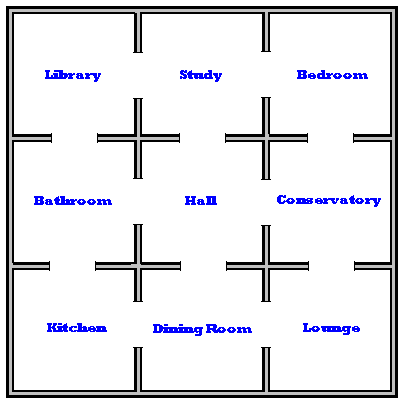
A student is dressed to look like the murderer(!) and stands on the
carpet piece marked "Hall".
A teacher (acting as Sherlock Holmes) explains that the murderer will be
tracked down in the house and arrested. Sherlock is blindfolded.
A second student throws the dice and states the number on the dice out loud.
The murderer walks through that many doors on the plan of the house.
Sherlock says "I know the murderer is not in the kitchen (or name of other
room) , so will someone please take away the kitchen"
A third student takes away the piece of carpet labelled "kitchen". the
murder from now on cannot step on the area which was once the kitchen.
The process is repeated a number of times until Sherlock can say "I know
that the murderer is in the ........... (name of room), you are under
arrest.
"How does the trick work?"
Well if the murderer starts in the hall, four rooms are one door away
(study, bathroom, dining room and conservatory). We shall call these rooms
odd rooms.
The other rooms are two doors away. We'll call these rooms even rooms.
If the number on the dice is even, Sherlock knows that the murderer must
have walked into an even room so can ask for one of the odd rooms to be
removed.
The process continues. Sherlock uses the principles that:
Odd + odd = even
Even + even = even
Even + odd = odd
Odd + even = odd
... to keep track of the rooms the murderer can't be in. By process of
elimination the correct room can be found (In practice Sherlock must reserve
the right not to remove a room in certain cases)
This could be followed by whole group discussion about how the trick was
performed (using student's own theories and words.
Students in pairs try to perform the trick using the a diagram and a counter
to represent the murderer.
Acting as Sherlock requires a great mental effort keeping track of the
rooms.
A number of items can be memorised in order by associating each item with
a place on a familiar journey.
For example 20 geometric shapes could be visualised at various places on the
journey from bed to school each morning. The shapes could be visualised at
places such as the bathroom, kitchen bus stop etc.
Students challenge each other to memorise the order and names of 20 shapes
such as pyramid, sphere, octagon etc.
One technique for remembering a list of items in order is by associating each item with an item from the following children's rhyme:
One is bun
Two is shoe
Three is tree
Four is door
Five is hive
Six is sticks
Seven is heaven
Eight is gate
Nine is line
Ten is pen etc.
This activity could start by collecting from the students a list of ten
popular video films. Students are then asked to conjure up in their minds a
crazy image of the item from the list above involved in the action of the
film.
Eg if the fifth film is The Sound of Music; a student might picture Julie
Andrews being chased over the Austrian Mountains by a swarm of angry bees.
Working in pairs students could practice this technique by memorising ten
items from a shopping list
Many mind reading tricks involve a "plant" in the audience secretly giving information to the mind reader. The way this information is given often involves mathematical codes or systems.
Nine objects are arranged in a 3 by 3 grid formation

While the magician isn't looking, the students are asked to choose an
object an concentrate on it. The magician can quickly identify the chosen
object by feeling the thought vibrations coming from it ... well not really.
One of the students has previously been asked to act as the "plant" giving
the magician a secret sign. Students are asked to work out some secret signs
which could correctly identify one of the nine objects.
One system could be that the plant and the magician agree to define each
object in terms of its row and column (like a matrix). The plant uses the
position of their head to indicate the row and arms to indicate the column.
Students are encouraged to invent similar (more complex) illusions.
(alternatively this trick could be performed using nine buckets placed
upside down on the floor with an item being put under one while the magician
isn't looking.)
"Black Magic" is a well known old party trick
in which a person apparently mind reads to find an object previously
selected by an audience. An accomplice helps by pointing to various objects
asking "is this it?". The mind reader always says no till after the
accomplice has pointed to a black object; the next object to be pointed out
will be the chosen object.
Students could devise similar mind reading tricks using number codes of
other systems.
One person thinks of a number 1 - 20. They are asked which cards contain their number. The magician can work out the number by adding up the top left numbers on each of the selected cards.

How does it work? The numbers in the top left of each card are powers of two and any number can be expressed as a combination of powers of two. this can be shown to be the basis of the binary system.
This trick could be described by a teacher without showing the students a set of cards. Students challenged to make their own set of cards and extend for numbers greater than 20 (the trick works better the more numbers there are on each card). Students should practice performing this trick on each other using their own set of cards
Here's a more detailed Interactive version
The Online Psychic
Wouldn't it be impressive if you could instantly write down a 4x4 magic
square giving any total that a friend suggests. It can be done ... there's a
trick to it!
First you have to memorise the basic 4x4 magic square which gives a total of
34. (Memorising this could lead to some interesting multisensory work!)
| 14 | 1 | 12 | 7 |
| 11 | 8 | 13 | 2 |
| 5 | 10 | 3 | 16 |
| 4 | 15 | 6 | 9 |
Let's suppose your friend chooses the number 57. Firstly subtract 33 from
this giving 24.
Now replace the numbers 1, 2, 3 and 4 in the basic square with 24, 25, 26
and 27 in that order.
You now have a magic square with 57 as the sum of each column, each row,
each diagonal and each 2 by 2 square within the larger square.
Why does this work? Look at the positions of the numbers 1 - 4. How are they
significant?
See also the Magic Square Puzzle.
I remember showing the trick above to my classes many years ago when I was trying to show off the magical powers that all Maths teachers have! So recently I was amazed to see another Magic Square trick on a YouTube video that used a totally different method based on binary numbers.
The trick featured in the video is John Walton’s Magic Square, also known as "Da Vinci Outnumbered".
The entire trick is based on 16 double-sided cards arranged in a 4x4 grid, allowing the magician to adjust the total on the fly based on the number the audience creates.
The 16 cards are pre-assigned into four distinct groups. These groups allow the magician to adjust the final total of the magic square by any value from 1 to 15 (or from 3 to 18 as the sum of three dice):
This system works by combining these differences, the magician can create any adjustment value needed (e.g., to increase the total by 7, he flips Group 1 + Group 2 + Group 4 cards, since 1 + 2 + 4 = 7).
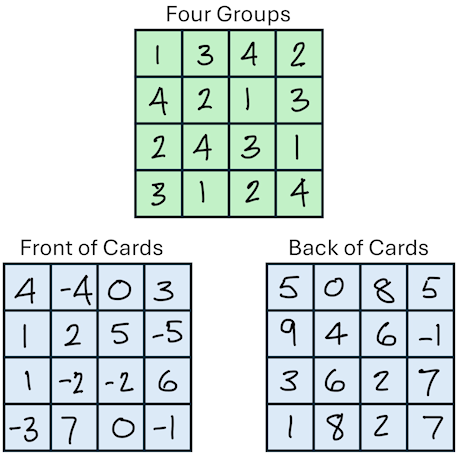
I'm not sure if my interpretation of the method exactly matches John Walton's but here is how it is performed:
The secret described in the video is a complex, yet elegant, application of Maths and misdirection that earned John Walton a "Fool Us" trophy.
The effect is that a pupil comes up with a three digit number and you challenge them to perform a calculation on that number using a calculator. You are always able to find the answer faster than thay can work it out.
The calculation involves multiplying the three digit number by 7, then the product is multiplied by 11 and then 13.
While the pupil is busy pressing buttons on the calculator you write down the three digit number twice to produce a six digit number which is the correct answer.
Example: 619
619 x 7 x 11 x 13
= 619619
It works because 7x11x13 is 1001.
Ask a friend to hold an odd number of coins in one hand and an even number of coins in the other but not to let you see. You will be able to work out in which hand the odd number of coins is hidden.

Ask the friend to multiply the number of coins in their left hand by three and the number of coins in their right hand by four then add the two totals together.
If the sum of their totals is odd then the odd number of coins is in their left hand otherwise the odd number of coins is in their right hand.
For a clue to realising why this trick works see Mix and Math.
Finally, a trick that is guaranteed to impress everyone you show it to. A trick people will beg you to show them how it works. This trick is truly mathemagical.

As this is the last trick in our collection we will let you ponder over it and discover the method for yourself. It is simple mathematics and if you try it enough times, keeping a record of your results, the secret will become clear. Good luck!
Here are some of the other magical(?) areas of the Transum Maths website:
Comment recorded on the i asp?ID_Top 'Starter of the Day' page by Ros, Belize:
"A really awesome website! Teachers and students are learning in such a fun way! Keep it up..."
Comment recorded on the 11 January 'Starter of the Day' page by S Johnson, The King John School:
"We recently had an afternoon on accelerated learning.This linked really well and prompted a discussion about learning styles and short term memory."
Comment recorded on the 17 November 'Starter of the Day' page by Amy Thay, Coventry:
"Thank you so much for your wonderful site. I have so much material to use in class and inspire me to try something a little different more often. I am going to show my maths department your website and encourage them to use it too. How lovely that you have compiled such a great resource to help teachers and pupils.
Thanks again"
Comment recorded on the 25 June 'Starter of the Day' page by Inger.kisby@herts and essex.herts.sch.uk, :
"We all love your starters. It is so good to have such a collection. We use them for all age groups and abilities. Have particularly enjoyed KIM's game, as we have not used that for Mathematics before. Keep up the good work and thank you very much
Best wishes from Inger Kisby"
Comment recorded on the 6 May 'Starter of the Day' page by Natalie, London:
"I am thankful for providing such wonderful starters. They are of immence help and the students enjoy them very much. These starters have saved my time and have made my lessons enjoyable."
Comment recorded on the 19 November 'Starter of the Day' page by Lesley Sewell, Ysgol Aberconwy, Wales:
"A Maths colleague introduced me to your web site and I love to use it. The questions are so varied I can use them with all of my classes, I even let year 13 have a go at some of them. I like being able to access Starters for the whole month so I can use favourites with classes I see at different times of the week. Thanks."
Comment recorded on the 7 April 'Starter of the Day' page by Marta, Rosea:
"Hello! I wanted to comment that these starters always brighten my day. My students and I are very grateful to have access to these resources. Thank you!"
Comment recorded on the 1 May 'Starter of the Day' page by Phil Anthony, Head of Maths, Stourport High School:
"What a brilliant website. We have just started to use the 'starter-of-the-day' in our yr9 lessons to try them out before we change from a high school to a secondary school in September. This is one of the best resources on-line we have found. The kids and staff love it. Well done an thank you very much for making my maths lessons more interesting and fun."
Comment recorded on the 24 May 'Starter of the Day' page by Ruth Seward, Hagley Park Sports College:
"Find the starters wonderful; students enjoy them and often want to use the idea generated by the starter in other parts of the lesson. Keep up the good work"
Comment recorded on the 16 March 'Starter of the Day' page by Mrs A Milton, Ysgol Ardudwy:
"I have used your starters for 3 years now and would not have a lesson without one! Fantastic way to engage the pupils at the start of a lesson."
Comment recorded on the 10 September 'Starter of the Day' page by Carol, Sheffield PArk Academy:
"3 NQTs in the department, I'm new subject leader in this new academy - Starters R Great!! Lovely resource for stimulating learning and getting eveyone off to a good start. Thank you!!"
Comment recorded on the 14 September 'Starter of the Day' page by Trish Bailey, Kingstone School:
"This is a great memory aid which could be used for formulae or key facts etc - in any subject area. The PICTURE is such an aid to remembering where each number or group of numbers is - my pupils love it!
Thanks"
Comment recorded on the 23 September 'Starter of the Day' page by Judy, Chatsmore CHS:
"This triangle starter is excellent. I have used it with all of my ks3 and ks4 classes and they are all totally focused when counting the triangles."
Comment recorded on the 28 September 'Starter of the Day' page by Malcolm P, Dorset:
"A set of real life savers!!
Keep it up and thank you!"
Comment recorded on the 3 October 'Starter of the Day' page by S Mirza, Park High School, Colne:
"Very good starters, help pupils settle very well in maths classroom."
Do you have any thoughts about the mathemagic above? Do you know any mathemagical tricks that we could share with the world on this page? Click on the link below to submit your ideas.
Click here to enter your comments.
D. Boyce, Rohwell
Monday, August 26, 2013
This has saved me a lot of time over my summer holidays - thank you.
Sadhana Bhat, Mpsmkbh@gmail.com
Saturday, October 19, 2013
Thank you and blessings.
Lisa Chalmers, Twitter
Sunday, September 6, 2015
I did the collaborative choice 'trick' with yr7 last lesson Friday. Answer in an envelope. They whooped!
Kyle D Evans, Maths Tricks To Blow Your Mind
Monday, May 30, 2022
On your calculator, multiply together ten random single-digit numbers. You can use the same number more than once. You should now have a fairly long number. Cover the first digit and add up all the other digits. Now you either have a single-digit number or a two-digit number. If you have a single-digit number, move to the next step. If you have a two-digit number, add those digits to make a single-digit number, then move to the next step. Subtract your number from 9. Now uncover the digit you’ve been covering. Ta-dah!
Transum,
Friday, October 27, 2023
October 31st is widely recognized as World Magic Day! It is also Halloween. This special day offers a perfect opportunity to delve into the enchanting world of 'Mathemagic.' Let the wonders of numbers bewitch you this Halloween!
World Magic Day is a day dedicated to the art of magic and the magicians who perform it. The day has a connection to the most famous magician, Harry Houdini, who died on October 31st, 1926. National Magic Day is celebrated in the United States and is part of National Magic Week, which is dedicated to celebrating the art of illusion and the craft of magicians everywhere. Magic shows with magicians and their assistants doing disappearing acts and pulling rabbits out of hats may seem to be something of our time, but magic as we know it today actually has its origins in ancient Egypt when the first conjuring act was recorded.
Missy, USA
Friday, April 11, 2025
The Times Eleven doesn't work if the numbers add up to 10 or more, unless you do an extra step. If the two digits add up to a number over 9, keep the second digit in the answer and add a 1 to the digit to the left.
Example 1: 538x11 = 5_8_11_8 = 5918 (I kept the 1 from the 11 and added 1 to the 8)
Example 2: 987x11 = 9_17_15_7 = 10857 (I kept the 5 from the 15 and added 1 to the 17, then kept the 8 from the 18 and added 1 to the 9).