Cookies are used on this website.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

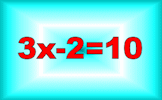• Equations A series of exercises, in increasing order of difficulty, requiring you to solve linear equations. The exercises are self marking.
• eQuation Generator An unlimited supply of linear equations just waiting to be solved. Project for the whole class to see then insert the working in your own style.
• Nevertheless Players decide where to place the cards to make an equation with the largest possible solution.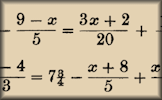
• Old Equations Solve these linear equations that appeared in a book called A Graduated Series of Exercises in Elementary Algebra by Rev George Farncomb Wright published in 1857.
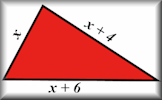• Algebraic Perimeters Questions about the perimeters and areas of polygons given as algebraic expressions.
• Missing Lengths Find the unknown lengths in the given diagrams and learn some algebra at the same time.
• Algebra In Action Real life problems adapted from an old Mathematics textbook which can be solved using algebra.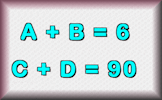
• Superfluous Find a strategy to figure out the values of the letters used in these calculations.
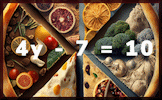• Solve To Find Fractions Find the value of the unknown in each of these linear equations. All of the answers are fractions
• Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level.
• Equations with Fractions Video If you have learnt how to solve linear equations the next step is to solve equations with fractions.
• Algebraic Fractions A mixture of algebraic fraction calculations and simplifications.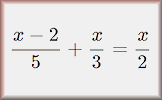
• Equations with Fractions Practise solving linear equations that contain fractions in this multi-level exercise.

Here are some exam-style questions on this statement:

• "Solve the following linear equations showing clearly each step of your working." ... more
• "The diagram shows an isosceles triangle (not drawn to scale)." ... more
• "The perimeter of the triangle is the same length as the perimeter of the square." ... more
• "Solve the following equation to find the value of \(x\)." ... more
• "Simplify the following algebraic fraction:" ... more
• "Aimee, Natasha and Ruby play hockey." ... more
• "Julie is on holiday and buys some fruit from the local market." ... more
• "Solve the following linear equation to find the value of \(x\)." ... more
• "The trapezium and rectangle shown here have the same perimeters. The diagrams are not drawn to scale and the measurements are in centimetres. Calculate the area of the trapezium." ... more
• "Two rectangles, not drawn to scale, are shown below. All measurements are in centimetres. Both rectangles have the same areas. Work out the perimeter of the rectangle on the left." ... more
• "(a) Solve." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".