

March 14th is π Day.
The third month and the 14th day
relates to 3.14 which is π to three
significant figures.
Today's challenge is to memorise π to as many digits as you can before it fades completely.
3.141592653589793238462643383279
502884197169399375105820
974944592307816406286
208998628034825
3421170679
...

Though it is not necessary for students to memorise pi these days it is important that they are familiar with it and can use a rough approximation of it to estimate answers to questions. This exercise certainly helps students become familiar with pi but also uses pi as an arbitrary subject of this memory challenge.
Incidently, in the days when memorising pi was important people devised mnemonics such as “How I wish I could calculate pi” where the number of letters in each word represent the first seven digits of pi. Do you know any other mnemonics for remembering pi? Please let us know.
Here is the URL which will take them to Transum's Pi-Mon game about memorising pi.
Topics: Starter | Circles | Memory | Multiple Intelligences | Rounding
If you cut the crust off a pizza pie and lay it across four others. You’ll see that the crust spans a little more than 3 pies.
— Pranay Pathole (@PPathole) March 14, 2021
That’s Pi ˜ 3.14. pic.twitter.com/QrMIHTsTOZ
OK - One more smile: Coffie and Pi for math nerds pic.twitter.com/UfvQjdjhu5
— Paul A. Kirschner (@P_A_Kirschner) February 6, 2022
happy pi day everyonepic.twitter.com/5CClCZDShq
— yuki (@shotawatanabes) March 13, 2022
How did you use this starter? Can you suggest
how teachers could present or develop this resource? Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for Maths teachers anywhere in the world.
Click here to enter your comments.
Previous Day | This starter is for 14 March | Next Day

|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=March14 However it would be better to assign one of the student interactive activities below. |
|
Here is the URL which will take them to a related student activity.
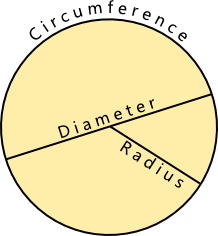
How does the circumference of a glass compare to the height of the glass? You'll be surprised when you find out.

Where \(e\) is Euler's number, the base of natural logarithms (2.718...) and
\(i\) is the imaginary unit, the square root of negative one.
First discovered by the Indian mathematician Madhava of Sangamagrama in the 14th century
then adapted and published by Gottfried Leibniz around 1676.
The normal distribution is the most important continuous distribution in
statistics and the graph is sometimes more commonly referred to as the bell-shaped curve.
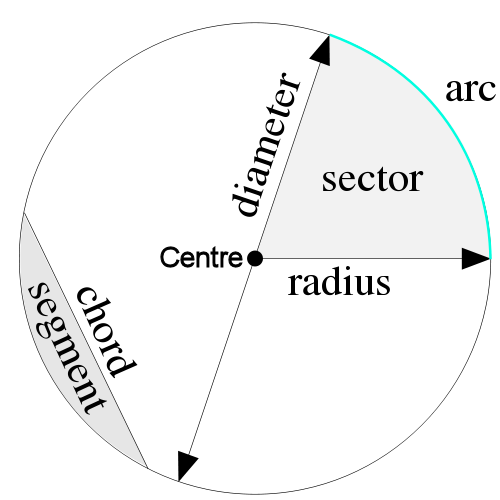
drop \(n\) needles of length \(L\) onto a plane ruled with parallel lines \(t\) units apart.
Count the number of needles, \(h\), that cross lines.
First posed by Mengoli in 1650 and solved by Euler in 1734 this is known as The Basel problem.
Even calculus has a use for pi as can be seen in this integration.
I didn't know you could find the factorial of a fraction.

Matt Parker's new book is all about our mistakes and misadventures with maths, geometry and all things numbers. Going from the mundane as to arguments about how many days in a week and the shape of footballs on signs, to famous errors and mistakes like the Space Shuttle disaster, London's walkie talkie building and the Millennium wobbly bridge. He explains how these problems occurred and in the case of some that they had occured in the past and we hadn't learnt from previous experience.
Originally a maths teacher from Australia, Matt Parker now lives in Godalming in a house full of almost every retro video-game console ever made. He is fluent in binary and could write your name in a sequence of noughts and ones in seconds. He loves doing maths and stand-up, often simultaneously.
You can find out more about this book here
Matt Parker gets involved in some amazing mathematical events including this historic record attempt:
Another amazing fact from Mr Pi Day, aka Chris Smith, MBE
AsapSCIENCE presents The Pi Song (Memorize 100 Digits Of π) - Wonderful!
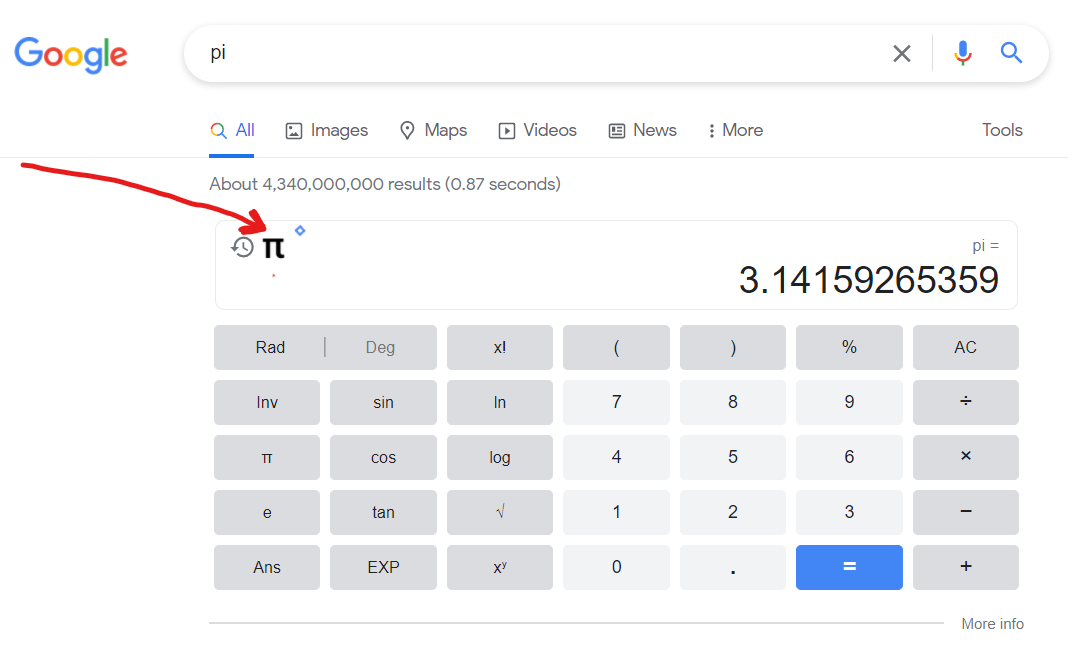
Type pi into the Google search engine page in your browser. Click the π symbol (I've drawn a red arrow pointing to it) and the game will begin. The value of pi will appear to ever increasing levels of accuracy which you then have to type back into the calculator. Your score will appear at the top left. How far can you get?

I am glad that Pi is pronounced to rhyme with eye!
Three hundred and fourteen people were asked what first
springs to mind when dividing the circumference of a circle by its diameter.
Organise a celebration with your friends or classmates to honour Pi Day. You could bake Pi-themed cakes, make Pi decorations, and even have a Pi-themed quiz or game.
\(\pi\)
Use the idea at the top of this page in which students recite as many digits of Pi as they can. This is a fun and challenging way to test your memory and compete with friends. I, of course, would like to recommend PiMon
\(\pi\)
Imagine dropping needles on a grid of parallel lines, where the distance between each line is greater than the length of a needle. Then, calculate the probability of the needles crossing one of the lines. Believe it or not, this probability is directly connected to the value of pi! [Research Buffon's Needle for more information]
\(\pi\)
Use the number Pi to create art, such as a Pi collage or a Pi-themed painting. You could even use the digits of Pi to create a digital art piece.
\(\pi\)
Cut strips of paper, write the digits of Pi on each strip, and link them together as if they were train trucks to create a Pi train. The longer the train, the better!
\(\pi\)
Celebrate Pi Day by baking a delicious (but healthy) pie with a mathematical theme. You could make a pie with a Pi symbol on top, or create a pie that incorporates the number Pi into the recipe.
\(\pi\)
Make a short video about Pi Day, explaining what it is and why it's important. You could include fun facts about Pi (see ideas above), demonstrations of how to calculate Pi, or interviews with people about what they think of Pi.
\(\pi\)
Set up a scavenger hunt with clues that lead to different locations around your school or community, with each clue containing a mathematical puzzle or challenge related to Pi.
\(\pi\)
Organize a Pi Day trivia game where students compete to answer questions about Pi, mathematics, and science. You could even offer prizes to the winners.
\(\pi\)
Encourage everyone to come to school dressed in Pi-themed attire, such as clothes with the Pi symbol or Pi-themed hats. (I did dress up as Piscine, the character from 'Life of Pi', as a tongue-in-cheek maths reference for World Book Day many years ago but I'm sure you could do better than that!)
\(\pi\)
Use Pi Day as an opportunity to raise money for a charity or cause that you care about. You could sell Pi-themed merchandise, host a bake sale, or organise a fun run or walk (3.14km) to raise funds for your chosen cause. The target for your fundraising could be £31.42, or £314.16 ($31.42, or $314.16)
Have you ever written any computer code? Here's an example of a JavaScript function that uses the Leibniz formula to estimate the value of pi:
function estimatePi(iterations) {
let pi = 0;
let sign = 1;
let denominator = 1;
for (let i = 0; i < iterations; i++) {
pi += sign * 4 / denominator;
sign *= -1;
denominator += 2;
}
return pi;
}
This function takes a single parameter called 'iterations', which specifies how many iterations of the series expansion to perform. The more iterations you use, the more accurate the estimate will be.
Note that this implementation uses the Leibniz formula, which converges relatively slowly. There are other series expansions that converge more quickly, but they can be more complex to implement.
Try it (note that the larger number of iterations will require a lot of your computer's processing power and may slow down normal operations!):

The expression on the image of a calculator above is an approximation of Ramanujan's formula, named after the Indian mathematician Srinivasa Ramanujan. Ramanujan discovered this formula in the early 20th century and it is one of the many impressive mathematical discoveries he made during his short life.
Interestingly, the value of the expression is accurate to 9 decimal places of pi, which is quite impressive given its simplicity.