|
|
|
Throw 2 dice and multiply the scores. Investigate!
What about 3 dice?
What about adding?
See also Snail Race, Dice Bingo, Dice and Spinners, and Probability.
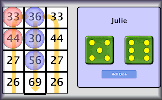
Here are some tables that you can type into. They may help with your investigation.
| Score | Frequency | Probability |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | ||
| 29 | ||
| 30 | ||
| 31 | ||
| 32 | ||
| 33 | ||
| 34 | ||
| 35 | ||
| 36 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
Sign in to your Transum subscription account to see the teacher Notes.
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
A mathematical investigation is quite different to other mathematical activities. The best investigations are open ended and allow students to choose the way they work and how they record their findings. It is one of the few occasions when 'going off on a tangent' is not only acceptable but actively encouraged (within reason).
Students may ask for 'the answers' but this supposes that the activity is
closed. Investigations can always be extended by varying the initial
instructions or asking the question 'what if...?'. Sometimes students point out
that the instructions are ambiguous and can be interpreted in different ways.
This is fine and the students are encouraged to explain how they interpreted the
instructions in their report.
Some students may benefit from a writing frame when producing the reports
of their investigations. Teachers may suggest sections or headings such as
Introduction, Interpretation, Research, Working and Conclusion or something
similar.
Featured ActivityOnline Logo An opportunity for students to write a computer program. There is nothing to download, all of the interaction takes place in the browser. Great for understanding angles and the properties of shapes. |
Recently UpdatedCoins and Notes Sharpen your money management skills by accurately calculating sums and working out change. So far this activity has been accessed 240 times and 24 Transum Trophies have been awarded for completing it. |
