The numbers in the circles add up to the numbers
in the rectangles between them.
Type in the missing numbers according to the rule.
You can earn a Transum Trophy for correctly completing eight arithmagons at any one level.
You are currently working on Level 7: One single digit number given in a circle and two numbers shown in rectangles. The numbers in the rectangles are the product of the two adjacent circle numbers.
You have earned a trophy for this level but there are more levels for you to try!
By working through these challenges you will discover the hidden secrets of Arithmagons. You will find the connections between the numbers in rectangles and the numbers in circles and in doing so develop strategies for solving the more difficult Arithmagon puzzles.
This activity is suitable for pupils of a wide range of abilities. It provides purposeful numeracy practice and levels that are a multiple of four (Level 4, Level 8, Level 12 etc.) encourage pupils to devise efficient solving strategies.
|
The subtraction or difference Arithmagons with only the rectangle numbers given (Levels 12, 24, 36 and 48) have an infinite number of correct solutions and the computer will allow any one of these correct solutions. In his pdf eBook Rich Starting Points for A Level Core Mathematics www.risps.co.uk Jonny Griffiths says that "there is no better way to present ideas of doing and undoing than arithmogons. They have been around a long time: 1975 is the first reference I have for them, but I daresay they have been around longer than that. One of their many marvellous aspects is that they require few words. John Mason and Sue Johnston-Wilder (Designing and Using Mathematical Tasks) give a long and fascinating study of how simple arithmogons can be used in a variety of ways." |
If your pupils do not have access to computers there is a printable set of Arithmagon worksheets here:
If you like Arithmagons you might also like these activities:
FractionsFractionagons Same structure as Arithmagons but designed to help pupils develop their fraction arithmetic. |
AlgebraAlgebragons Same structure as Arithmagons but designed to help pupils develop their algebra skills |
PuzzlePentadd Quiz Find the five numbers which when added or multiplied together in pairs to produce the given sums or products. |
There are many more puzzles on the Transum Puzzle page.
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Do you know the origin of the title 'Arithmagons'? This activity has been used in schools for many years but who is the person we should thank for dreaming up the idea?
Still looking for a challenge? Try one of these activities:
Ming GameSuko Sujiko Interactive number-based logic puzzles similar to those featuring in daily newspapers. |
ChallengeSatisfaction This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers. |
SuggestedMagic Square Puzzle Find all of the possible ways of making the magic total from the numbers in this four by four magic square. |
There are many more puzzles on the Transum Puzzle page.
The solutions to this and other Transum puzzles, exercises and activities are available here when you are signed in to your Transum subscription account. If you do not yet have an account and you are a teacher, tutor or parent you can apply for one by completing the form on the Sign Up page.
A Transum subscription also gives you access to the 'Class Admin' student management system, downloadable worksheets, many more teaching resources and opens up ad-free access to the Transum website for you and your pupils.
Close
| ◯ ◯ ◯ | ◯ ◯ ▭ | ◯ ▭ ▭ | ▭ ▭ ▭ | |
| 1 | Level 1 | Level 2 | Level 3 | Level 4 |
| 5 | Level 5 | Level 6 | Level 7 | Level 8 |
| 9 | Level 9 | Level 10 | Level 11 | Level 12 |
| ◯ ◯ ◯ | ◯ ◯ ▭ | ◯ ▭ ▭ | ▭ ▭ ▭ | |
| 13 | Level 13 | Level 14 | Level 15 | Level 16 |
| 17 | Level 17 | Level 18 | Level 19 | Level 20 |
| 21 | Level 21 | Level 22 | Level 23 | Level 24 |
| ◯ ◯ ◯ | ◯ ◯ ▭ | ◯ ▭ ▭ | ▭ ▭ ▭ | |
| 25 | Level 25 | Level 26 | Level 27 | Level 28 |
| 29 | Level 29 | Level 30 | Level 31 | Level 32 |
| 33 | Level 33 | Level 34 | Level 35 | Level 36 |
| ◯ ◯ ◯ | ◯ ◯ ▭ | ◯ ▭ ▭ | ▭ ▭ ▭ | |
| 37 | Level 37 | Level 38 | Level 39 | Level 40 |
| 41 | Level 41 | Level 42 | Level 43 | Level 44 |
| 45 | Level 45 | Level 46 | Level 47 | Level 48 |
The first Arithmagon you will see is a triangle with three circles at its vertices and rectangles on its sides. The idea is to add up the two numbers in circles at either end of a side of a triangle and type the answer into the rectangle on the middle of that side.
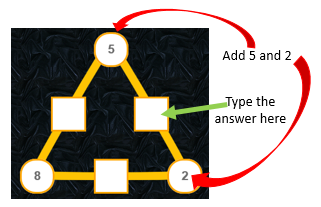
Click the check button when you have filled in all three rectangles. If you are correct you will see one slice of a pie chart showing your progress so far. Complete eight Arithmagons to earn a Transum Trophy.
This first level you should find very easy. It gets more difficult when you are not given the three circle numbers but are given the rectangle numbers instead. That’s when you need to come up with a strategy!
You are currently working on Level 7: One single digit number given in a circle and two numbers shown in rectangles. The numbers in the rectangles are the product of the two adjacent circle numbers.
Close
Transum,
Monday, June 2, 2014
"Don't be content with only completing the first level of this challenge, click the 'More Levels' tab to select more difficult puzzles. Try the 'Two digit numbers', 'Addition', 'Three rectangle values only' combination to produce some interesting arithmagons.."
Year 4, St Olave’s
Wednesday, November 14, 2018
Ben Winter, Winterteach
Wednesday, May 19, 2021
"Hi John, thanks again for all of the amazing activities on your website. I use them with my students and am really enjoying the arithmagons. They are a great way of allowing students to show their understanding of number facts and the relationship between addition and subtraction.
[Transum: Great to hear that Ben. Thanks so much for the feedback.]"