

Here are the six islands of Transumberg connected by nine bridges.
Can you find a route, starting on any of the islands, that crosses each bridge once?
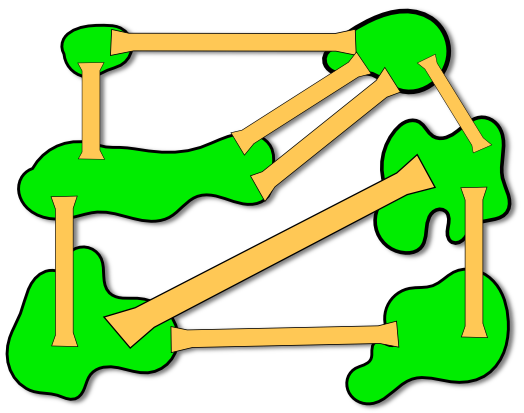
If you found that puzzle easy try this:
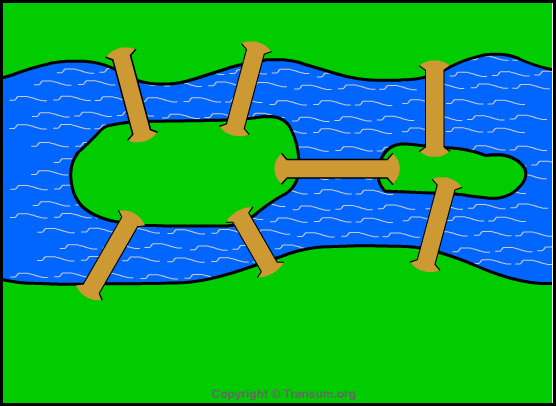
Can you find a route crossing each bridge once (and only once)?
Which town is this?
How did you use this starter? Can you suggest
how teachers could present or develop this resource? Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for Maths teachers anywhere in the world.
Click here to enter your comments.
Previous Day | This starter is for 6 August | Next Day
Sign in to your Transum subscription account to see the answers
Can you make up your own bridge crossing puzzle with a different number of bridges and islands. How can you predict if the puzzle will be impossible?
Your access to the majority of the Transum resources continues to be free but you can help support the continued growth of the website by doing your Amazon shopping using the links on this page. Below is an Amazon link. As an Amazon Associate I earn a small amount from qualifying purchases which helps pay for the upkeep of this website.
Educational Technology on Amazon

|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=August6 However it would be better to assign one of the student interactive activities below. |
|
Here is the URL which will take them to a similar type of puzzle.
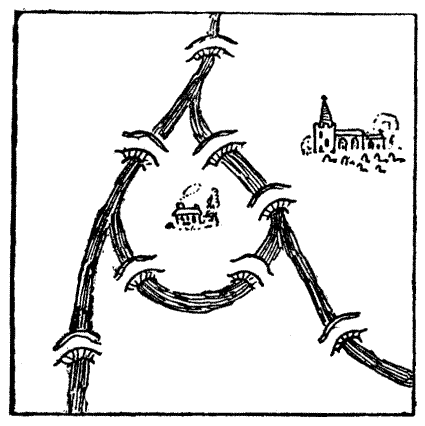
"Here, my worthy Pilgrims, is a strange riddle," quoth the Parson. "Behold how at the branching of the river is an island. Upon this island doth stand my own poor parsonage, and ye may all see the whereabouts of the village church. Mark ye, also, that there be eight bridges and no more over the river in my parish. On my way to church it is my wont to visit sundry of my flock, and in the doing thereof I do pass over every one of the eight bridges once and no more. Can any of ye find the path, after this manner, from the house to the church, without going out of the parish? Nay, nay, my friends, I do never cross the river in any boat, neither by swimming nor wading, nor do I go underground like unto the mole, nor fly in the air as doth the eagle; but only pass over by the[Pg 49] bridges." There is a way in which the Parson might have made this curious journey. Can the reader discover it? At first it seems impossible, but the conditions offer a loophole.
The Canterbury Puzzles, by Henry Ernest Dudeney
In the history of mathematics, the first person go on record with a proven statement about the second problem above was Leonhard Euler in 1736. His 'solution' is considered to be the first theorem of graph theory and the first true proof in the theory of networks, a subject now generally regarded as a branch of combinatorics.
In addition, Euler's recognition that the key information was the number of bridges and the list of their endpoints (rather than their exact positions) is the basis of topology. The difference between the actual layout and the graph schematic is a good example of the idea that topology is not concerned with the rigid shape of objects.