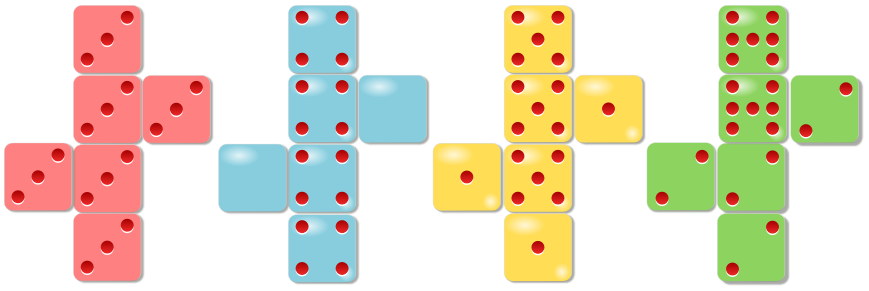
Imagine a game in which two people roll a dice and whoever gets the higher number wins. A prize is awarded to the person winning most times after 100 games.
The catch is the dice don’t have the numbers one to six on their faces. There are four different dice and you are allowed to choose which dice you will play with.
Which dice would you choose to give you the best chance of winning the prize?

