
 |
Exam-Style Questions on NumberProblems on Number adapted from questions set in previous Mathematics exams. |
2. | GCSE Higher |
Without using a calculator:
(a) Express 68 as the product of its prime factors.
(b) Divide 68 by 5 giving your answer in decimal format.
(c) Multiply 13.06 by 2.1
3. | GCSE Higher |
The number, \(N\), can be written as the product of prime factors in index form as:
$$N = 3 × 5^3 × x^4$$Work out \(5N^2\) as a product of prime factors in index form giving your answer in terms of \(x\).
4. | GCSE Higher |
The difference between the areas of the two squares is 51 cm2.
When measured in cm the lengths of the sides of the squares are integers and both less than 20cm.
Find the lengths of the sides of the two squares.
5. | IB Studies |
This Venn diagram shows the relationship between the sets of numbers
$$\mathbb N, \mathbb Z, \mathbb Q \text{ and } \mathbb R$$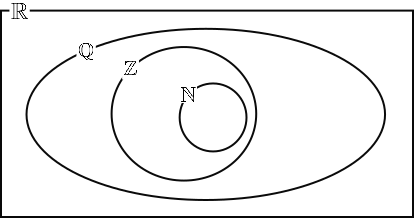
Write down the following numbers in the appropriate place in the Venn diagram.
(a) \(5\)
(b) \(\frac23\)
(c) \(\pi\)
(d) \(0.91\)
(e) \(\sqrt 7\)
(f) \(-0.75\)
6. | GCSE Higher |
This expression can be used to generate a sequence of numbers.
$$n^2+n + 5$$(a) Work out the first three terms of this sequence.
(b) What is the smallest value of \(n\) that produces a term of the sequence that is not a prime number?
(c) Is it true that odd square numbers have exactly three factors? Explain and justify your answer.
(d) Seymour is thinking of a number.
Find the two possible numbers that Seymour could be thinking of.
7. | IB Analysis and Approaches |
Consider \( w = a - bi \) where \( |w| = 1 \)
Show that \( \text{Re} \left( \frac{w + i}{w - i} \right) \) is always equal to 0.
8. | IB Analysis and Approaches |
A complex number, \(c\), has a real part \(1\) and an imaginary part \( -\sqrt{3} \).
(a) Show that \(c = 2e^{i\frac{5 \pi}{3}}\).
(b) Find the smallest positive integer \(n\) such that \( c^n\) is a real number.
(c) Find the value of \(c^n\) when \(n\) takes the value found in part (b).
Consider the equation \(z^3-9z^2+18z-28=0\), where \(z \in \mathbb{C} \).
(d) Given that \(c\) is a root of \(z^3-9z^2+18z-28=0\), find the other roots.
(e) By using a suitable transformation from \(z\) to \(w\), or otherwise, find the roots of the equation \(1-9w+18w^2-28w^3=0\), where \(w \in \mathbb{C} \).
Consider the equation \(z^2 = 2z^*\) , where \(z \in \mathbb{C}, z \neq 0 \).
(f) By expressing \(z\) in the form \(a + bi\), find the roots of the equation.
9. | IB Analysis and Approaches |
Consider \( P(z) = z^3 +2nz - \frac{40z^2}{n} - 10n\), where \( z \in \mathbb{C} \) and \( n \in \mathbb{R}^+ \).
Given that \( z - 4i \) is a factor of \( P(z) \), find the roots of \( P(z) = 0 \).
10. | IB Analysis and Approaches |
Consider the complex numbers \(z_1 = c + 3i\) and \(z_2 = c^2-2-ci\)
(a) Find an expression for \(z_1z_2 \) in terms of \(c\).
(b) Hence, given that arg(\(z_1z_2 \)) = \( \tan^{-1} 2 \) show that:
$$c^3 - c^2 + c + 3 = 0 $$If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.