|
|
Exam-Style Questions on InequalitiesProblems on Inequalities adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
The red line in the diagram below shows an inequality. If the variable is \(x\), which inequality best describes \(x\)?
(a) \(-9 \le x \le 4\)
(b) \(-9 \lt x \le 4\)
(c) \(-9 \le x \lt 4\)
(d) \(-9 \lt x \lt 4\)
(e) \(-4 \le x \le 9\)
2. | GCSE Higher |
(a) Write down the integer values of \(x\) that satisfy the inequality \(–3 \le x \lt 1 \).
(b) Solve the compound inequality \( -4 \leq 2y + 1 \lt 6 \) and write down the integer solutions for \(y\).
(c) Find the single digit integers for \(z\) which satisfy the inequality \( -3z \leq 9 \).
3. | GCSE Higher |
(a) Solve 9m < 15m − 12
(b) On the number line below, show the set of values of \(x\) for which \( -4 \le x-1 \lt 5 \)
4. | GCSE Higher |
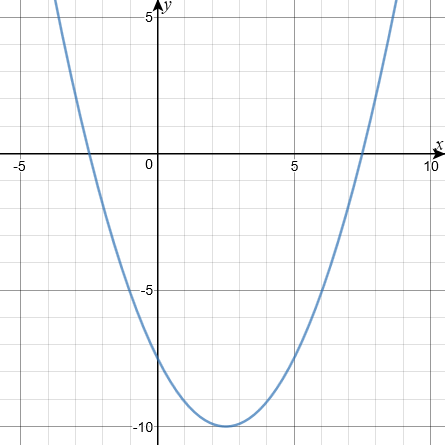
The graph of a quadratic function, \(y=f(x)\) is shown drawn accurately in the following diagram. Write down all the integer solutions of \(f(x) \le 0\).
5. | GCSE Higher |
The diagram below is a sketch of \(y = f(x)\) where \(f(x)\) is a quadratic function.
The graph intersects the x-axis where \(x=-2\) and \(x = 0.5\).
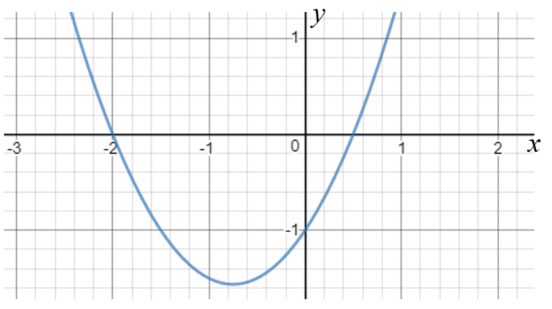
Which of the following is the solution of \(f(x) \le 0\) ?
6. | GCSE Higher |
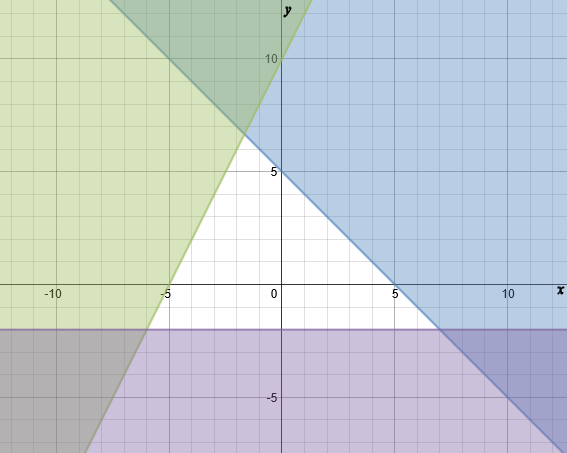
Describe the unshaded (white) region by writing down three inequalities.
7. | GCSE Higher |
On the grid below indicate the region that satisfies all three of these inequalities.
$$y>-2$$ $$x+y<5$$ $$y-1 \le \frac{x}{2}$$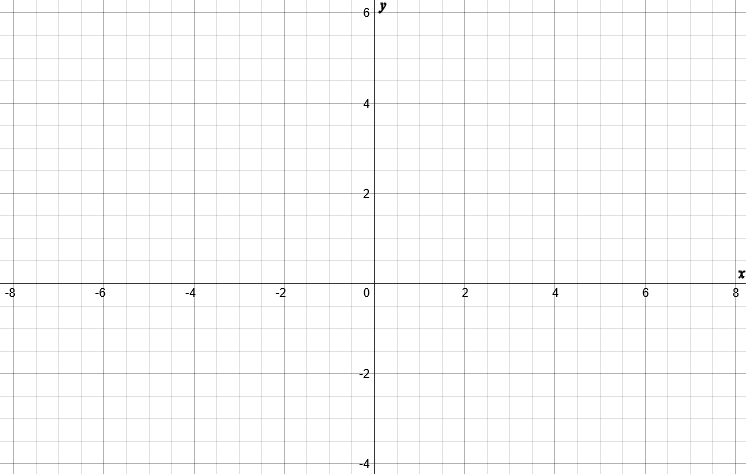
8. | GCSE Higher |
A region on a coordinate grid is described by the following three inequalities:
$$x>-2$$ $$x+y<7$$ $$y \ge \frac{x}{3}+2$$By shading the unwanted regions show the region on the grid below.
9. | GCSE Higher |
By shading the unwanted regions, show the region satisfied by these three inequalities.
$$ y \le x + 3 $$ $$ y> 4-x $$ $$ x < 2.5 $$
10. | GCSE Higher |
Solve the following inequalities then explain how the whole number solutions to A and B different.
$$A: 5 \le 5x \lt 30$$ $$B: 5 \lt 5x \le 30$$11. | GCSE Higher |
A region on a coordinate grid is described by the following three inequalities:
$$-8 \le x \le 6$$ $$2y \ge x + 1$$ $$2y+x \le 12$$(a) By shading the unwanted regions show the region on the grid below.
(b) Mr Mushnik says that the point with coordinates (-8, 10) does not satisfy all the inequalities because it does not lie in the region. Is Mr Mushnik correct? You must give a reason for your answer.
12. | GCSE Higher |
Show that you understand equations and inequalities by answering the following:
(a) Solve \(5x^2=80\)
(b) Solve \(8x + 2 \gt x + 7\)
(c) Write down the largest integer that satisfies \(8x - 2 \lt 25\)
(d) Solve the following pair of equations
$$3x + 5y = 21$$ $$8x - 5y = 1$$13. | GCSE Higher |
John times how long it takes him to run around Hazelnut Park each Friday afternoon. The last three weeks his times, rounded to the nearest minute are \(p, q \; \text{and} \; r\).
He notices that \(q\) is 5% more than \(p\) and \(r\) is 5% less than \(q\).
Indicate which of the following statements are true:
(a) \( r \lt p \) and \( r \lt q \)
(b) \( r \gt p \) and \( r \gt q \)
(c) \( r = p \) and \( r \lt q \)
(d) \( p \gt q \) and \( p = r \)
(e) \( p =q \) and \( p \gt r \)
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
