
 |
Exam-Style Questions on CorrelationProblems on Correlation adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
The number of visitors to a cycle track and the number of drinks sold by a café at the location are recorded in the table below.
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday | |
| Numver of visitors | 32 | 45 | 39 | 43 | 58 | 84 | 65 |
| Drinks sold | 17 | 20 | 23 | 7 | 24 | 49 | 38 |
The data is shown in the following scatter diagram:
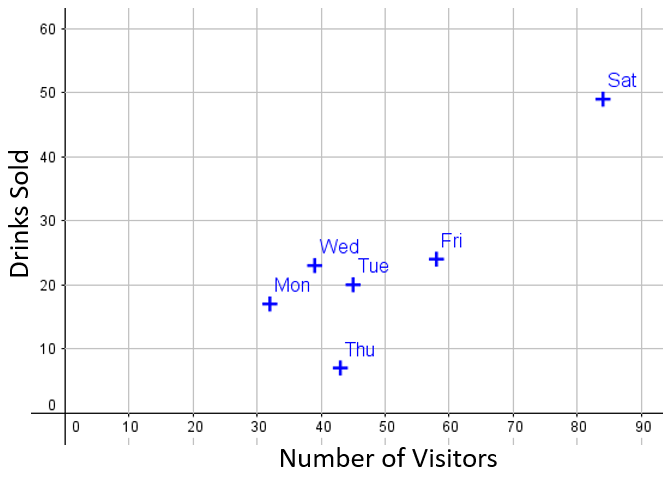
(a) Add Sunday's data to the scatter diagram.
(b) Draw, by eye, a line of best fit on the scatter diagram.
(c) Describe the relationship between the number of visitors and the number of drinks sold.
(d) Which particular day does not fit the relationship?
(e) If one day there were 50 visitors, estimate how many drinks would be sold.
2. | GCSE Higher |
The scatter graph shows the maximum temperature (oC) and the number of bowls of soup sold at a sandwich shop on twelve randomly selected days last year.
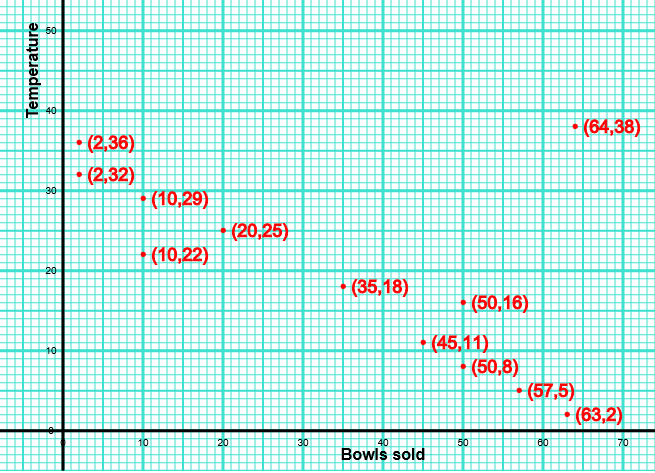
(a) One of the points is an outlier. What temperature does this outlier represent.
(b) For all the other points write down the type of correlation.
(c) On another day of the year, the temperature was 20oC. Estimate the number of bowls of soup sold on that day.
(d) The shop owner says "We sell more bowls of soup the higher the temperature". Does the scatter graph support this statement? Give a reason for your answer.
3. | GCSE Higher |
In the Bubbleless Bandits free-diving club, members practice breath-holding techniques as part of their routine.

In this club, the older members have been practicing these techniques for many years, leading to increased breath-holding capacity through disciplined training and improved technique. The older members tend to be the more experienced free-divers. They have mastered relaxation and breath control, contributing to their ability to hold their breath for longer periods.
The times, \( t \) seconds, that club members could hold their breath while diving and their ages, \( x \) years, are recorded. The results are shown in the table.
| Age, \( x \) years | Time, \( t \) seconds |
|---|---|
| 19 | 37 |
| 31 | 44 |
| 55 | 101 |
| 33 | 63 |
| 29 | 55 |
| 61 | 110 |
| 40 | 78 |
| 35 | 71 |
(a) Draw a scatter diagram to represent this data.
(b) What type of correlation is shown on the scatter diagram?
(c) Find the equation of the regression line giving your answer in the form \( t = ax + b \).
(d) Use your regression equation to estimate the time a person aged 45 could hold their breath.
(e) Give a reason why you should not use the regression equation to estimate the time it would take a person aged 14 to do the task.
4. | IB Studies |
The following table shows the relationship between the number of workers and the amount of time in minutes it takes them to harvest the sugar cane in a particular field.
| Workers (\(n\)) | Time (\(t\)) |
|---|---|
| 3 | 799 |
| 4 | 703 |
| 5 | 645 |
| 6 | 570 |
| 8 | 422 |
| 9 | 322 |
| 10 | 241 |
(a) Find the equation of the regression line of \(t\) on \(n\).
(b) Find the value of the Pearson’s product–moment correlation coefficient, r.
(c) Use the regression equation to find how long it would take seven workers to harvest the sugar cane.
5. | IB Standard |
The following table shows the amount of diesel required by a train to travel certain distances.
| Distance (\(x\) km) | 90 | 150 | 230 | 310 | 390 |
|---|---|---|---|---|---|
| Diesel used (\(y\) litres) | 19.2 | 33.9 | 49.0 | 79.5 | 89.9 |
This data can be modelled by the regression line with equation \(y=ax+b\).
(a) Find the values of \(a\) and of \(b\).
(b) Explain what the gradient \(a\) represents.
(c) Use the model to estimate the amount of diesel the train would use if it is driven 270 km.
6. | IB Standard |
The following table shows the weight in kilograms of members of a group of young children of various ages.
| Age (x years) | 1.6 | 2.5 | 3.3 | 4.4 | 5.6 |
|---|---|---|---|---|---|
| Weight ( y kg) | 12 | 15 | 16 | 17 | 20 |
The relationship between the variables is modelled by the regression line with equation \(y = ax + b\)
(a) Find the value of \(a\) and of \(b\)
(b) Write down the correlation coefficient.
(c) Use your equation to estimate the mean weight of a child that is four years old.
7. | IB Standard |
The following table shows the average number of hours per night sleeping by seven men and their youngest child.
| Hours sleep per night of father (x) | 6.7 | 7.1 | 7.2 | 7.9 | 8.1 | 8.2 | 8.2 |
| Hours sleep per night of youngest child (y) | 7.9 | 8.0 | 8.5 | 8.7 | 9.1 | 9.2 | 9.5 |
The relationship can be modelled by a regression line with equation \(y = mx + c\).
(a) Find the correlation coefficient.
(b) Write down the value of \(m\) and of \(c\).
(c) Young Ramin sleeps for an average of 8.6 hours per day. Use your regression line to predict the average number of hours his father sleeps. Give your answer in hours and minutes correct to the nearest minute.
8. | IB Analysis and Approaches |
A programmer recorded the number of web pages she had created since she had begun working for the Corney Content Creation Company. The following table shows the number of days, \(d\), and the cumulative total number of web pages, \(p\).
| Number of days \((d)\) | 5 | 9 | 16 | 18 | 23 | 29 | 32 | 40 | 50 |
| Number of pages \((p)\) | 14 | 28 | 47 | 54 | 65 | 90 | 95 | 123 | 156 |
The value of Pearson's product moment correlation coefficient, \(r\) for this data is 0.999 to three significant figures.
(a) The regression line of \(p\) on \(d\) for this data can be written in the form \(p=ad + b\). Find the value of a and the value of b.
(b) Use your regression line to estimate the number of web pages created by day 45.

9. | IB Standard |
The following table shows the average weights for given heights in a population of men.
| Heights (x cm) | 160 | 165 | 170 | 175 | 180 | 185 |
| Weights ( y kg) | 65.1 | 67.9 | 70.1 | 72.8 | 75.4 | 77.2 |
(a) The relationship between the variables is modelled by the regression equation \(y = ax + b\). Write down the value of \(a\) and of \(b\).
(b) Use this relationship to estimate the weight of a man whose height is 177 cm.
(c) Find the correlation coefficient.
(d) State which two of the following describe the correlation between the variables.
10. | IB Analysis and Approaches |
Ten students are given a test on calculus and a test on probability. Each test is scored out of a total of 100 marks. The scores of the students are shown in the following table:

| Student | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Calculus | 50 | 68 | 98 | 90 | 79 | 78 | 85 | 99 | 69 | 59 |
| Probability | 56 | 74 | 96 | 90 | 81 | 80 | 87 | 98 | 74 | 66 |
Let \( x \) be the score on the calculus test and \( y \) be the score on the probability test.
The teacher finds that the equation of the regression line of \( y \) on \( x \) for these scores is
$$ y = 0.815x + 17.1 $$
(a) Find the value of Pearson’s product-moment correlation coefficient, \( r \).
Jaidee was absent for the calculus test and Permsak was absent for the probability test.
The teacher uses the regression line of \( y \) on \( x \) to estimate the missing scores.
Permsak scored 15 on the calculus test.
The teacher estimated his score on the probability test to be 29 to the nearest integer using the following calculation:
$$ y = 0.815(15) + 17.1 \approx 29 $$
(b) Give a reason why this method is not appropriate for Permsak.
Jaidee scored 85 on the probability test.
(c) Use an appropriate method to show that the estimated calculus test score for Jaidee is 83 to the nearest integer.
11. | IB Studies |
As part of a conservation project, Darren was asked to measure the circumference of trees that were growing at different distances from a beach.
His results are shown in the following table.
| Distance, \(x\) (metres) | 6 | 14 | 20 | 25 | 35 | 48 | 46 | 48 | 52 |
| Circumference, \(y\) (centimetres) | 52 | 57 | 57 | 68 | 65 | 70 | 75 | 80 | 82 |
(a) State whether distance from the beach is a continuous or discrete variable.
(b) On graph paper, draw a scatter diagram to show Darren’s results. Use a scale of 1 cm to represent 5 m on the x-axis and 1 cm to represent 10 cm on the y-axis.
(c) Calculate the mean distance, \(\bar x\) , of the trees from the beach.
(d) Work out the mean circumference, \(\bar y\) , of the trees.
(e) Plot and label the point M(\(\bar x,\bar y\)) on your graph.
(f) Write down the Pearson’s product–moment correlation coefficient, \(r\) , for Darren's results.
(g) Find the equation of the regression line \(y\) on \(x\), for Darren’s results.
(h) Draw the regression line \(y\) on \(x\) on your graph.
(i) Use the equation of the regression line \(y\) on \(x\) to estimate the circumference of a tree that is 42 m from the beach.
12. | IB Analysis and Approaches |
At a large airport, the waiting time between a plane landing and a passenger being able to get off the aircraft is dependent upon the row number of the seat that the passenger has been assigned to.
Betty, a frequent flier, took a flight to the airport on seven consecutive weekends. The following table shows the row number, \( x \), and Betty's waiting time, \( y \) minutes.
| Row number (\( x \)) | Betty’s waiting time (\( y \)) |
|---|---|
| 43 | 18 |
| 50 | 27 |
| 36 | 16 |
| 39 | 20 |
| 58 | 30 |
| 54 | 25 |
| 36 | 19 |
The relationship between \( x \) and \( y \) can be modelled by the regression line of \( y \) on \( x \) with equation \( y = mx + b \).
(a) Find the value of \( m \) and the value of \( b \).
(b) Write down the value of Pearson’s product-moment correlation coefficient, \( r \).
(c) Interpret, in context, the value of \( m \) found in part (a).
On another week, Betty takes the same flight. She has been assigned 42C, a seat in the forty second row.
(d) Use the result from part (a) to estimate Betty’s waiting time to leave the aircraft after it has landed.
13. | IB Applications and Interpretation |
The Farang Parkour Team hosted a Free Running event. The judges, Anan and Jason awarded 7 competitors a score out of 10. The scores are shown in the following table.
| Free Runners | A | B | C | D | E | F | G |
| Anan's Score (x) | 7.8 | 9.1 | 8.3 | 6.9 | 7.0 | 8.5 | 9.3 |
| Jason's Score (y) | 7.2 | 9.0 | 8.7 | 7.5 | 6.9 | 8.7 | 8.9 |
(a) Find the Pearson’s product–moment correlation coefficient, \(r\), of these scores.
(b) Using the value of \(r\), interpret the relationship between Anan’s scores and Jason’s score.
(c) Write down the equation of the regression line \(y\) on \(x\).
(d) Use your regression equation from part (c) to estimate Jason’s score to one decimal place when Anan awards a score of 5.
(e) State whether this estimate is reliable. Justify your answer.
(f) The adjudicator for the event would like to find the Spearman’s rank correlation coefficient of the scores. Copy and complete the information in the following table.
| Free Runners | A | B | C | D | E | F | G |
| Anan's Rank | 7 | 1 | |||||
| Jason's Rank | 1 | 7 |
(g) Find the value of the Spearman’s rank correlation coefficient, \(r_s\).
(h) Comment on the result obtained for \(r_s\).
The adjudicator believes Jason’s score for competitor E is too high and so decreases the score from 6.9 to 6.5.
(i) Explain why the value of the Spearman’s rank correlation coefficient \(r_s\) does not change.
14. | IB Studies |
In a survey of insect life near a stream, a student collected data about the number of different insect species \((y)\) that were found at different distances \((x)\) in metres from the stream.
| Distance \((x)\) | 2 | 5 | 8 | 11 | 14 | 17 | 22 | 33 | 39 |
|---|---|---|---|---|---|---|---|---|---|
| Insect species \((y)\) | 26 | 25 | 19 | 19 | 14 | 9 | 5 | 3 | 2 |
(a) Draw a scatter diagram to show the data.
(b) Using your scatter diagram, describe the correlation between the number of different insect species and the distance from the stream.
(c) Find \(\bar x\), the mean of the distances from the stream;
(d) Find \(\bar y\), the mean number of insect species.
(e) Plot the point \((\bar x,\bar y)\) on your scatter diagram. Label this point M.
(f) Write down the equation of the regression line \(y\) on \(x\) for the above data.
(g) Draw the regression line \(y\) on \(x\) on your scatter diagram.
(h) Estimate the number of insect species to be found 30 metres from the stream.
15. | IB Analysis and Approaches |
A pair of twins, Percy and Patsy, take Maths assessment tests each week. Their teacher records their scores in this table:
| Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | Week 6 | Week 7 | Week 8 | |
|---|---|---|---|---|---|---|---|---|
| Percy (\(x\)) | 52 | 60 | 58 | 61 | 65 | 60 | 70 | 72 |
| Patsy (\(y\)) | 50 | 60 | 61 | 59 | 64 | 64 | 68 | 73 |
(a) Find an equation of the regression line of \(x\) on \(y\). The equation should be written in the form \(x = ay + b\).
(b) Find an equation of the regression line of \(y\) on \(x\). The equation should be written in the form \(y = ax + b\)
(c) Find the coordinates of the point of intersection of these two lines.
16. | IB Studies |
The table below shows the scores for 12 students on two Mathematic exam papers. For the first paper calculators were allowed and for the second paper they were not.
| Paper 1 (\(x\)) | 74 | 73 | 65 | 75 | 68 | 72 | 69 | 71 | 83 | 68 | 68 | 73 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Paper 2 (\(y\)) | 75 | 83 | 69 | 77 | 71 | 77 | 68 | 76 | 84 | 69 | 71 | 75 |
(a) Write down the mean score on Paper 1.
(b) Write down the standard deviation of the scores for Paper 1.
(c) Find the number of students that had a score of more than one standard deviation below the mean on Paper 1.
(d) Write down the correlation coefficient, \(r\).
(e) Write down the equation of the regression line of \(y\) on \(x\).
Another student scored 75 on Paper 1.
(f) Calculate an estimate of his score on Paper 2
Another student scored 88 on Paper 1.
(g) Determine whether you can use the equation of the regression line to estimate his score on Paper 2. Give a reason for your answer.
17. | IB Analysis and Approaches |
A community leader is monitoring the state of flood water levels in a local area.
The depth of the flood water is recorded on seven different days.
The following table shows the number of days, \( d \), since the monitoring began and the average depth, \( h \) cm, of the flood water on each of those days.
The value of Pearson’s product-moment correlation coefficient, \( r \), for this data is -0.991, correct to three significant figures.
$$ \begin{array}{|c|c|} \hline \text{Number of days } (d) & \text{Average height } (h) \\ \hline 1 & 24.5 \\ 3 & 18.1 \\ 4 & 15.3 \\ 6 & 11.7 \\ 7 & 10.3 \\ 9 & 5.9 \\ 11 & 2.9 \\ \hline \end{array} $$(a) The regression line of \( h \) on \( d \) for this data can be written in the form \( h = ad + b \).
Find the value of \( a \) and the value of \( b \).
(b) Use your regression line to estimate the average height of the plants when the experiment has been running for 8 days.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.