
 |
Exam-Style Questions on CircleProblems on Circle adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
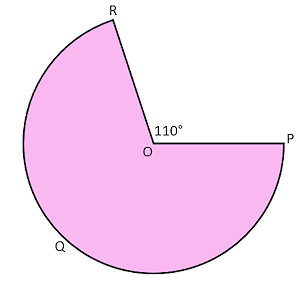
The diagram shows a sector of a circle, centre O, with one angle shown as being 110°. If the radius of the circle is 8cm calculate:
(a) The area of the shaded area.
(b) The perimeter of the shaded area.
2. | GCSE Higher |
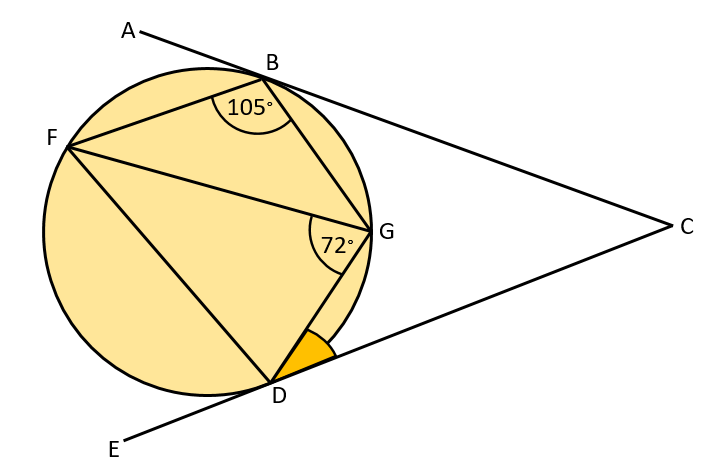
Points B, D, G and F lie on a circle.
ABC is the tangent to the circle at B.
CDE is the tangent to the circle at D.
Find the size of angle CDG.
You must give a reason for each stage of your working.
3. | GCSE Higher |
OAB is a sector of a circle with centre O and radius 10 cm.
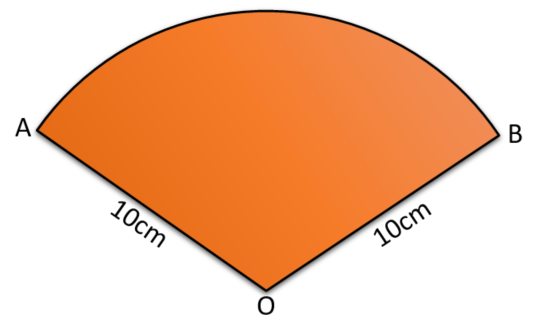
The length of the arc from A to B is 15cm.
Calculate the are of the sector. Give your answer correct to 3 significant figures.
4. | GCSE Higher |
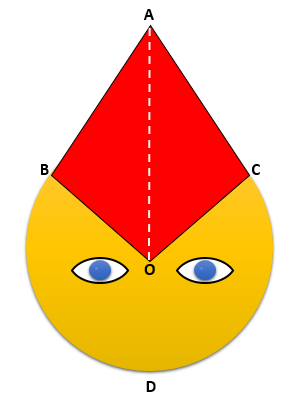
This draft emoji design (not drawn to scale) includes a circle and a kite.
AB and AC are both tangents to the circle centre O.
The radius of the circle is 7cm. The dashed line AO is 12cm.
Calculate the length of the arc BDC.
5. | GCSE Higher |
What is the equation of a circle, centered at the origin, that has a tangent passing through the points (-30, 0) and (0, -15)?
Show all of your working.
6. | GCSE Higher |
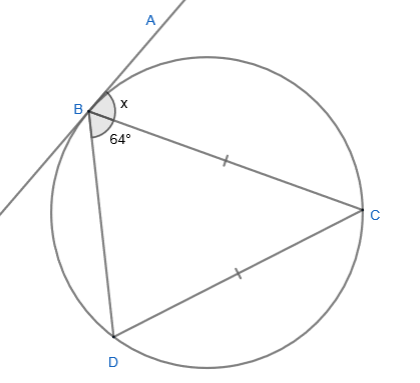
(a) Find \(x\), the size of angle ABC if B, C and D are all points on the circle to which AB is a tangent. The diagram is not drawn to scale.
(b) Give a reason for your answer
7. | GCSE Higher |
The diagram shows a circle with equation \(x^2+y^2=13\).
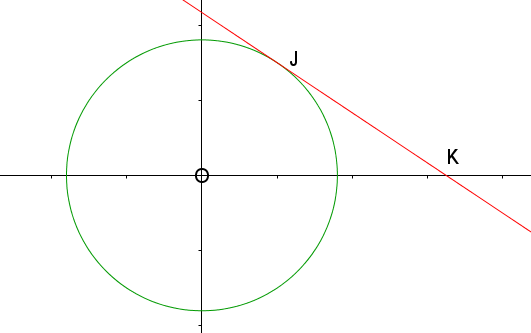
A tangent to the circle touches the circle at the point J. The x-coordinate of J is 2. The tangent intersects the x-axis at K. Find the coordinates of the point K.
8. | GCSE Higher |
(a) Find the coordinates of the point at which the curve \(y = k^x\) intersects the y-axis.
The equation of circle \(A\) is \(x^2+y^2=25\). This circle is translated by the vector \( \begin{pmatrix} 0 \\ 4 \\ \end{pmatrix} \) to give circle \(B\).
(b) Draw a sketch of circle \(B\) clearly labelling the points of intersection with the y-axis.
9. | GCSE Higher |
A circle with equation \(x^2 + y^2 = 6 \) meets a one of its tangents at point \(S\).
The coordinates of \(S\) are:
$$\left( \frac{\sqrt 5}{3} , \frac{7}{3} \right)$$Find the equation of the tangent to the circle at the point \(S\).
10. | GCSE Higher |
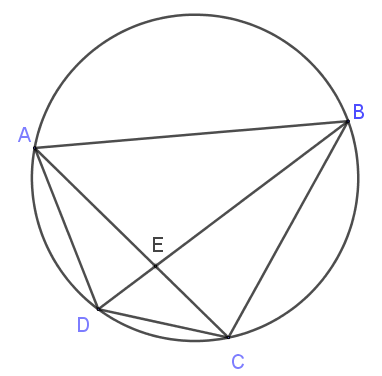
The diagram, not drawn to scale, shows chords joining points on the circumference of a circle. Prove that triangle ADE is similar to triangle BCE.
11. | IB Standard |
The following diagram shows a circle with centre O and radius 9 cm.
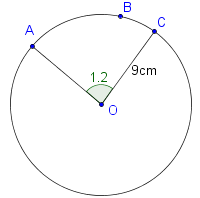
The points A, B and C lie on the circumference of the circle, and AÔC = 1.2 radians.
(a) Find the length of the arc ABC.
(b) Find the perimeter of the minor sector OAC.
(c) Find the area of the minor sector OAC.
12. | GCSE Higher |
Two identical small yellow circles are drawn inside one large circle, as shown in the diagram. The centres of the small circles lie on the diameter of the large circle. The part of the large circle that is outside both small circles is painted red.
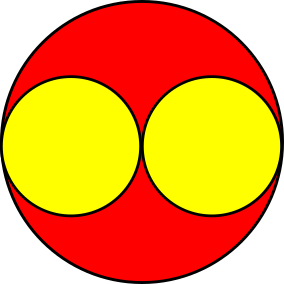
Find the fraction of the large circle that is painted red.
13. | GCSE Higher |
(a) The circumference of a circle is \(16 \pi \) cm and its centre is at the origin. Find the equation of the circle.
(b) The line \(12x+ ay = b\) is a tangent at the point (6, 5) to a different circle with centre at the origin. Find the values of a and b.
14. | IB Analysis and Approaches |
The diagram shows a circle with a minor sector shaded blue and a major sector shaded yellow.
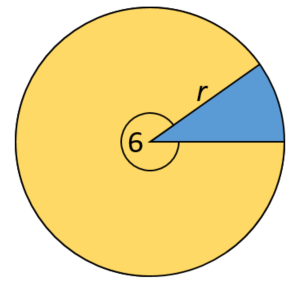
The angle subtended by the major sector at the centre of the circle is six radians.
The perimeter of the major sector is 32.
(a) Find the value of r.
(b) Hence find the exact area of the minor sector.
15. | IB Standard |
The diagram below shows an isosceles right-angled triangle and two arcs of circles. The larger arc is part of a circle with its centre at D and the smaller arc is part of a circle with its centre at A.
The right-angled triangle has two sides of length 10cm.
The point D is the midpoint of BC.
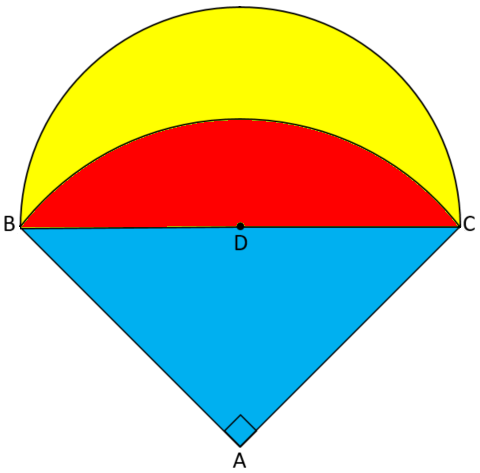
(a) Calculate the area of the red segment.
(b) Calculate the area of the yellow region.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.