Snail Race

This is a visual aid designed to be projected onto a whiteboard for whole class exposition (Tip: Press the F11 key for full screen view). A printable version is here.

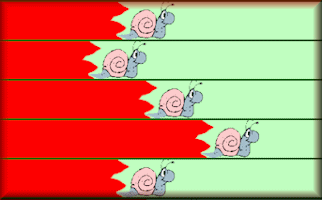
Two dice are rolled and the sum calculated. The snail with that number takes one step forwards. The first snail to the end of the race track wins. Before playing the students could be asked to predict which snail will win. Twelve students could be asked to volunteer to be the 'trainers' for each of the snails, their names can be typed into the spaces provided above.

This activity could be followed by the students producing the possibility space for the sums of two dice.

Students could then design their own race boards and make predictions:

• Turtle Race: In which dice scores are subtracted
• Snake Race: In which the dices scores are multiplied
• Penguin Race: In which three dice are used.

How did you use this resource?
Can you suggest how teachers could present or develop this resource?