Note to teacher: Doing this activity once with a class helps students develop strategies. It is only when they do this activity a second time that they will have the opportunity to practise those strategies. That is when the learning is consolidated. Click the button above to regenerate another version of this starter from random numbers.
Answers
Sign in to your Transum subscription account to see the answers
Christmas Present Ideas
It is often very difficult choosing Christmas presents for family and friends but so here are some seasonal, mathematics-related gifts chosen and recommended by Transum Mathematics.
Go Genius MathsTransform maths practice into an exciting adventure with Go Genius Maths! This award-winning board game is designed to make learning maths enjoyable and engaging for children aged 7 and above. Perfect for family game nights or classroom activities, Go Genius Maths helps players develop essential arithmetic skills while having heaps of fun. Whether you’re looking for a gift to inspire young minds or a tool to supplement maths education, Go Genius Maths is the ultimate choice. Spark curiosity, nurture mathematical talent, and turn learning into an unforgettable journey! |
|
||||
|
How Not To Be WrongThe maths we learn in school can seem like an abstract set of rules, laid down by the ancients and not to be questioned. In fact, Jordan Ellenberg shows us, maths touches on everything we do, and a little mathematical knowledge reveals the hidden structures that lie beneath the world's messy and chaotic surface. In How Not to be Wrong, Ellenberg explores the mathematician's method of analyzing life, from the everyday to the cosmic, showing us which numbers to defend, which ones to ignore, and when to change the equation entirely. Along the way, he explains calculus in a single page, describes Gödel's theorem using only one-syllable words, and reveals how early you actually need to get to the airport. What more could the inquisitive adult want for Christmas? This book makes a cosy, interesting read in front of the fire on those cold winter evenings. more... #ad |
||||
Graphic Display CalculatorThis handheld device and companion software are designed to generate opportunities for classroom exploration and to promote greater understanding of core concepts in the mathematics and science classroom. TI-Nspire technology has been developed through sound classroom research which shows that "linked multiple representation are crucial in development of conceptual understanding and it is feasible only through use of a technology such as TI-Nspire, which provides simultaneous, dynamically linked representations of graphs, equations, data, and verbal explanations, such that a change in one representation is immediately reflected in the others. For the young people in your life this is a great investment. Bought as a Christmas present but useful for many years to come as the young person turns into an A-level candidate then works their way through university. more... #ad |
|
||||
|
Apple iPad ProThe analytics show that more and more people are accessing Transum Mathematics via an iPad as it is so portable and responsive. The iPad has so many other uses in addition to solving Transum's puzzles and challenges and it would make an excellent gift for anyone. The redesigned Retina display is as stunning to look at as it is to touch. It all comes with iOS, the world's most advanced mobile operating system. iPad Pro. Everything you want modern computing to be. more... #ad Before giving an iPad as a Christmas gift you could add a link to iPad Maths to the home screen. |
||||
Craig Barton's Tips for TeachersTeaching is complex. But there are simple ideas we can enact to help our teaching be more effective. This book contains over 400 such ideas." more... #ad "The ideas come from two sources. First, from the wonderful guests on his Tips for Teachers podcast - education heavyweights such as Dylan Wiliam, Daisy Christodoulou and Tom Sherrington, as well as talented teachers who are not household names but have so much wisdom to share. Then there's what he has learned from working with amazing teachers and students in hundreds of schools around the world. |
|
||||
|
The Story Of Maths [DVD]The films in this ambitious series offer clear, accessible explanations of important mathematical ideas but are also packed with engaging anecdotes, fascinating biographical details, and pivotal episodes in the lives of the great mathematicians. Engaging, enlightening and entertaining, the series gives viewers new and often surprising insights into the central importance of mathematics, establishing this discipline to be one of humanity s greatest cultural achievements. This DVD contains all four programmes from the BBC series. Marcus du Sautoy's wonderful programmes make a perfect Christmas gift more... #ad |
||||
Christmas MathsThis book provides a wealth of fun activities with a Christmas theme. Each photocopiable worksheet is matched to the Numeracy Strategy and compatible with the Scottish 5-14 Guidelines. This series is designed for busy teachers in the late Autumn term who are desperate for materials that are relevant and interesting and that can be completed with minimun supervision. All the activities are suitable for use by class teachers, supply teachers, SEN teachers and classroom assistants and cover topics such as 'How many partridges did the true love give all together?' and 'Filling a sleigh with presents by rolling a dice!'. Children will have lots of fun working through the Christmas Maths themes but also gain valuable skills along the way. A great source of ideas and another reasonably priced stocking filler. more... #ad |
|
||||
|
A Compendium Of Mathematical MethodsHow many different methods do you know to solve simultaneous equations? To multiply decimals? To find the nth term of a sequence? A Compendium of Mathematical Methods brings together over one hundred different approaches from classrooms all over the world, giving curious mathematicians the opportunity to explore fascinating methods that they've never before encountered. If you teach mathematics to any age group in any country, you are guaranteed to learn lots of new things from this delightful book. It will deepen your subject knowledge and enhance your teaching, whatever your existing level of expertise. It will inspire you to explore new approaches with your pupils and provide valuable guidance on explanations and misconceptions. more... #ad |
||||
Math with Bad DrawingsI had been tutoring the wonderful Betsy for five years. When the day came for our last ever session together before the end of her Year 13, I received this beautiful book as a gift of appreciation. This a very readable book by Ben Orlin. I'm really enjoying the humour in the writing and the drawings are great. Ben Orlin answers maths' three big questions: Why do I need to learn this? When am I ever going to use it? Why is it so hard? The answers come in various forms-cartoons, drawings, jokes, and the stories and insights of an empathetic teacher who believes that mathematics should belong to everyone. more... #ad |
|
||||
Click the images above to see all the details of these gift ideas and to buy them online.
Maths T-Shirts
Your access to the majority of the Transum resources continues to be free but you can help support the continued growth of the website by doing your Amazon shopping using the links on this page. Below is an Amazon link. As an Amazon Associate I earn a small amount from qualifying purchases which helps pay for the upkeep of this website.
Educational Technology on Amazon
|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=October25 However it would be better to assign one of the student interactive activities below. |
|
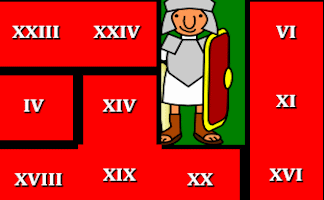
Here is the URL which will take them to an interactive jigsaw puzzle of Roman numerals.
If you are not an expert on Roman numerals here is an explanation:
| Symbol | Value |
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1,000 |
Numbers are formed by combining symbols together. So II is two ones, i.e. 2, and XIII is a ten and three ones, i.e. 13. There is no zero in this system, so 207, for example, is CCVII, using the symbols for two hundreds, a five and two ones. 1066 is MLXVI, one thousand, fifty and ten, a five and a one.
Symbols are placed from left to right in order of value, starting with the largest. However, in a few specific cases, to avoid four characters being repeated in succession (such as IIII or XXXX) these can be reduced using subtractive notation as follows:
- the numeral I can be placed before V and X to make 4 units (IV) and 9 units (IX) respectively
- X can be placed before L and C to make 40 (XL) and 90 (XC) respectively
- C can be placed before D and M to make 400 and 900 according to the same pattern
Explanation adapted from the Wikepedia article on Roman numerals.
Extension
 |
 |
 |
Which clockface is the odd one out?
The answer can be found by looking closely at the roman numerals used.
Riddle
What is my name?
Five hundred is at my end and at my start.
The number five is at my heart.
The first letter is second to appear,
But the first number completes me clear.
Challenge
Somewhere in London is a monument with a date in Roman numerals inscribed on its north side. The number contains each of the digits once each in order from M to I. The first person to send Transum a photograph of themselves in London in front of this inscription will win a nice prize.
The prize remains unclaimed as of today, Saturday 21st December 2024
Challenge Update 8th April 2022
Children in Year 5 of Whitchurch Primary in Oxford UK have had great fun exploring the site to complete their unit on a Roman numerals. They were excited to solve the challenge to do with the London monument. They used their super-smart research skills to work out which monument has the inscription and they even found a photograph of it on the web.
The children of Year 5 have not yet managed to get to London to take a prize winning photograph so the prize is still up for grabs!
Three members of the Year 5 class can be seen in the photograph above. Very well done and a special mention for Mr Chesters, their teacher.
