Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
Interest Practise using the formulas for simple interest and compound interest.
Interest Video Learn about simple interest, compound interest, appreciation and depreciation. This video is to help you do the online, self-marking exercise.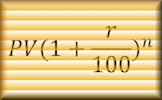
Compound Interest Calculator A customised online calculator for quickly finding the solutions to compound interest problems.
Here are some exam-style questions on this statement:
- "Elaine invests £150 000 in a savings account for six years." ... more
- "Winky Lash wants to invest £20 000 for 3 years in a bank. She has the following two choices of banks, both offering compound interest but on different terms:" ... more
- "The value of a boat is £220 000." ... more
- "The value of a new car is £22 000." ... more
- "Michael Banks invests £2000 in a savings account for two years. The account pays 2% compound interest per annum." ... more
- "The value of a new house, \(V\), is given by:" ... more
- "Here are the details for two bank accounts." ... more
- "Montague invests £7000 for six years in a bank offering compound interest at \(x%\) per annum." ... more
- "On Billy's 16th birthday his parents gave him options of how he might receive his monthly allowance for the next two years." ... more
- "All answers to this question should be given to the nearest whole currency unit." ... more
- "Two friends Arthur and Babette, each set themselves a target of saving £12000. They each have £6800 to invest." ... more
- "Ruby invests a certain amount of money in a bank account that pays a nominal annual interest rate of 6.7%, compounded quarterly." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Money For many pupils the ability to understand financial transactions is a skill they thank their mathematics teacher for. Understanding the use of money is a real, practical application of mathematics in the real world and is just as important today as ever it was. When it comes to managing our money and avoiding costly mistakes it is well worthwhile to strive to become an expert. There are key aspects of personal finance the pupils should understand as the get older and more independent in their lives and the activities provided here provide resources for a small part of their learning process.
- Sequences A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them. The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms. Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom. Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.
Furthermore
Compound interest is a fundamental concept in finance where the interest accrued on an amount of money is added to the original principal, forming a new base on which subsequent interest is calculated. This process allows interest to be earned on previously accumulated interest, leading to the amount growing exponentially over time.
The key formula for compound interest is:
$$ FV = PV \times \left( 1 + \frac{r}{100k} \right) ^{kn} \\ \text{where:} \\ FV \text{ is the future value of the investment/loan, including interest} \\ PV \text{ is the principal investment amount (the initial deposit or loan amount)} \\ r \text{ is the annual interest rate (r=6 means six percent)} \\ n \text{ is the number of years} \\ k \text{ is the number of times the interest is compounded per year.} $$For example, let's consider a principal amount (PV) of £1000, with an annual interest rate (r) of 5%, compounded quarterly (k=4) for 1 year (n=1). Using the compound interest formula, the future value (FV) would be calculated as follows:
$$ FV = £1000 \times \left( 1 + \frac{5}{400} \right) ^{4} \\ FV = £1000 \times (1.0125)^4 \\ FV \approx £1050.95 $$So, the investment would grow to approximately £1050.95 after one year with quarterly compounding.
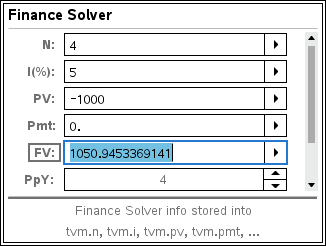
If you use the TI-Nspire graphic display calculator here are instructions for using the Finance Solver.
This video on Compound Interest and Depreciation is from Revision Village and is aimed at students taking the IB Maths Standard level course
This video on Finance Solver is from Revision Village and is aimed at students taking the IB Maths Standard level course.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
