|
|
Exam-Style Questions on EquationsProblems on Equations adapted from questions set in previous Mathematics exams. |
1. | IGCSE Core |
Nora and Dora are trying to solve the following simultaneous equations by finding the intersection of their graphs.
$$y+x=6$$ $$y-x=1$$Here are their graphs:
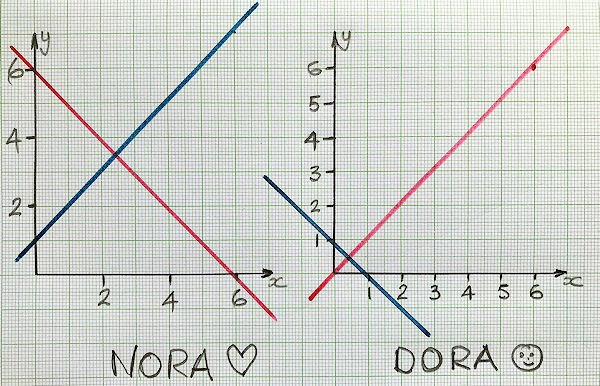
(a) Who has plotted the graphs most correctly?
(b) What is the correct solution?
2. | GCSE Higher |
Solve the following linear equation to find the value of \(x\).
$$ \frac{5x+4}{3} - \frac{2x-3}{5} = \frac{10+x}{2} $$3. | GCSE Higher |
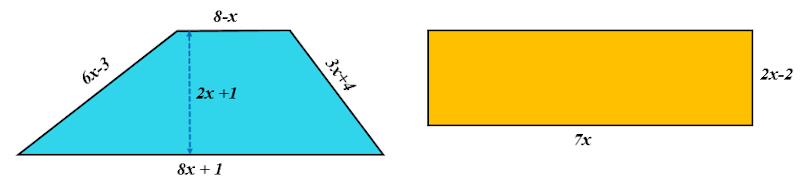
The trapezium and rectangle shown here have the same perimeters. The diagrams are not drawn to scale and the measurements are in centimetres. Calculate the area of the trapezium.
5. | GCSE Higher |
(a) Solve.
$$\frac{4w}{5} - 2 = 5\frac{1}{5}$$
(b) $$\frac{4(3^{-y})}{5} - 2 = 5\frac{1}{5}$$
Find the value of \( y \).
6. | GCSE Higher |
Estimate the solutions of the following simultaneous equations using their graphs as drawn on the grid below.
$$3x-5y=17$$ $$y=5-\frac{7x}{5}$$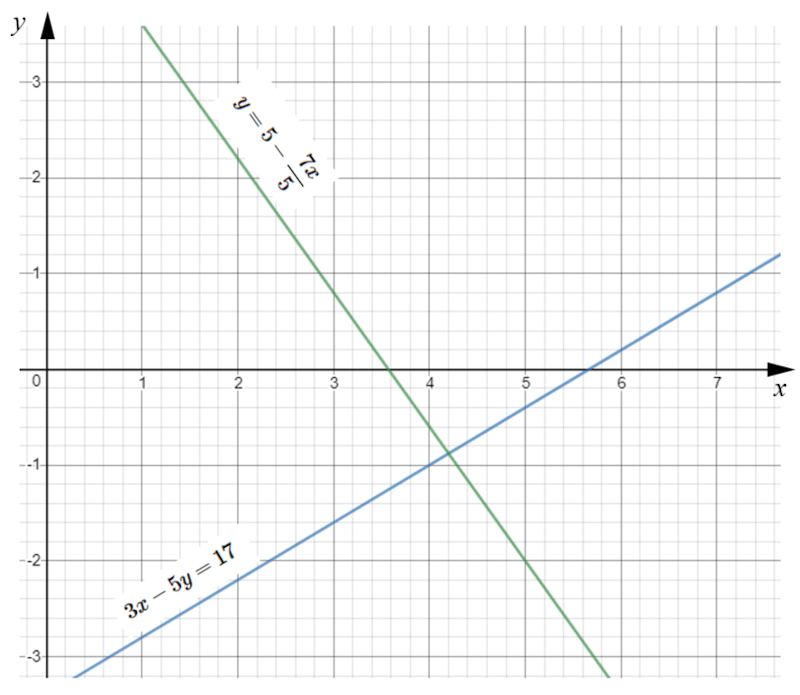
8. | IGCSE Extended |
(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\).
(b) Solve the equation \(3x^2-8x-5=0\) showing all of your working and giving answers to three significant figures.
(c) The total surface area of a cone with radius \(x\) and slant height \(8x\) is equal to the area of a circle with radius r. Show that \(r = 3x\).
[The curved surface area, \(A\), of a cone with radius \(r\) and slant height \(l\) is \(A=\pi rl\).]
9. | GCSE Higher |
A rectangular sheet of paper can be cut into two identical rectangular pieces in two different ways, either by cutting along line A or by cutting along line B.
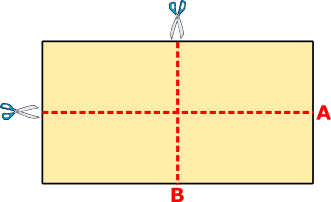
When the original sheet of paper is cut along line A, the perimeter of each of the two pieces is 56 cm.
When the original sheet of paper is cut along line B, the perimeter of each of the two pieces is 64 cm.
What is the perimeter of the original sheet of paper?
10. | GCSE Higher |
(a) Solve the simultaneous equations.
$$4p + 2q = 1$$
$$p - q = 1$$
(b) Hence, for \(0^\circ \leq u \leq 360^\circ\) and \(0^\circ \leq v \leq 360^\circ\), solve the simultaneous equations.
$$4\sin u + 2\cos v = 1$$
$$\sin u - \cos v = 1$$
11. | GCSE Higher |
Draw the graph of \(y = 2x^2 + 3x - 7\) for \( -3.5 \le x \le 2\). Draw suitable straight lines to find approximate solutions (to one decimal place) of the equations:
(a) \(2x^2 +3x - 9 = 0\)
(b) \(2x^2 +4x - 7 = 0\)
(c) \(2x^2 - x -5 = 3 - x\)
12. | IB Studies |
A red rug has a width of \(x-3\) cm and a length of \(4x\) cm.
(a) Write down an ex
The area of the rug is 3240 cm2.
(b) Calculate the value of \(x\).
(c) Hence, write down the value of the length and of the width of the rug in centimetres.
13. | GCSE Higher |
The diagram shows a circle with equation \(x^2+y^2=13\).
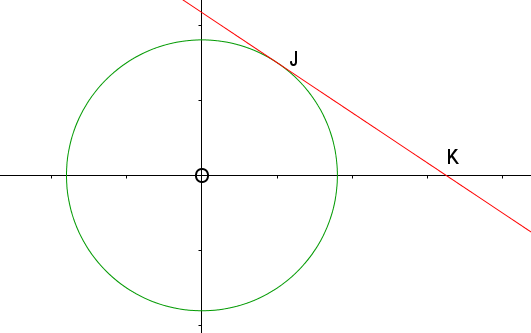
A tangent to the circle touches the circle at the point J. The x-coordinate of J is 2. The tangent intersects the x-axis at K. Find the coordinates of the point K.
14. | GCSE Higher |
(a) Find the coordinates of the point at which the curve \(y = k^x\) intersects the y-axis.
The equation of circle \(A\) is \(x^2+y^2=25\). This circle is translated by the vector \( \begin{pmatrix} 0 \\ 4 \\ \end{pmatrix} \) to give circle \(B\).
(b) Draw a sketch of circle \(B\) clearly labelling the points of intersection with the y-axis.
15. | GCSE Higher |
Solve algebraically the simultaneous equations to find the solution where \(-10 \le x \le 10\).
$$ 3x^2 - y^2 = 11 $$ $$ 5x + 3y = 27 $$16. | GCSE Higher |
A circle with equation \(x^2 + y^2 = 6 \) meets a one of its tangents at point \(S\).
The coordinates of \(S\) are:
$$\left( \frac{\sqrt 5}{3} , \frac{7}{3} \right)$$Find the equation of the tangent to the circle at the point \(S\).
17. | GCSE Higher |
Two numbers are chosen so that the sum of their squares is 25.
If those numbers are represented by \(x\) and \(y\) they will also satisfy the equation:
$$y-3x=13$$Use an algebraic method to find two possible values of \(x\) and \(y\) .
18. | GCSE Higher |
The prices of two watches are in the ratio \(a:b\).
When the prices are both increased by £10, the ratio becomes \(5 : 7\).
When the prices are both reduced by £10, the ratio becomes \(1 : 3\).
Express the ratio \(a:b\) in its lowest terms.
19. | GCSE Higher |
(a) The circumference of a circle is \(16 \pi \) cm and its centre is at the origin. Find the equation of the circle.
(b) The line \(12x+ ay = b\) is a tangent at the point (6, 5) to a different circle with centre at the origin. Find the values of a and b.
20. | IB Analysis and Approaches |
Solve for x where \( -\pi \le x \le \pi \).
$$ \sin{2x} = \cos{x} $$21. | IB Analysis and Approaches |
Find the range of possible values of \(a\) such that \(5e^x - \ln{a} = e^{2x}\) has at least one real solution.
22. | A-Level |
The curve C has parametric equations
\(x=2t+3, \quad y=7-2t^2\)
(a) Find the cartesian equation for C in its simplest form.
(b) Find \( \dfrac{dy}{dx} \)
The point \(P\) lies on C where \(t = 3\)
(c) Find the equation of the tangent to C at the point \(P\). Give your answer in the form \(y = ax + b\), where \(a\) and \(b\) are integers to be determined.
23. | IB Analysis and Approaches |
(a) Show that \(2x+15+\dfrac{40}{x-3}= \dfrac{2x^2+9x-5}{x-3}, \quad x \in \mathbb{R}, x \neq 3\)
(b) Hence or otherwise, solve the equation \( 2\cos{2\theta}+15+\dfrac{40}{\cos{2\theta}-3}=0, \quad \text{ for } 0 \le \theta \le \pi\)
24. | A-Level |
(a) Solve the following trigonometric equation for \(–360° \lt x \lt 360°\):
$$ 5 \sin^2 x + 2\sin x + 3 = 7 \cos^2 x $$giving your answers to the nearest integer.
(b) Hence find the smallest positive solution of the equation
$$ 5 \sin^2(3\theta + 20°) + 2\sin (3\theta + 20°) + 3 = 7 \cos^2 (3\theta + 20°) $$giving your answer to 2 decimal places.
25. | A-Level |
(a) Using a suitable substitution, or otherwise, find
$$ \int \frac{x}{(3x^2 - 5)^2} dx$$(b) Solve the differential equation below giving your answer in the form \(y = f(x)\). It is given that given that y = \( \frac{1}{2} \) when x = 0.
$$ \frac{dy}{dx} = \frac{2xy^3}{(3x^2 - 5)^2}$$26. | IB Analysis and Approaches |
Consider the differential equation \( \dfrac{dy}{dx} = \dfrac{xy+y^2}{x^2} \), where \( x \gt 0, y \gt 0 \).
It is given that \(y = 3 \) when \(x = 1\).
(a) Use Euler's method with step length \(0.1\) to find an approximate value of \(y\) when \(x=1.2\).
(b) By solving the differential equation, show that \( y = \frac{-x}{ \ln |x| + C } \)
(c) Find the value of \(y\) when \(x=1.2\).
(d) With reference to the concavity of the graph of \( y = \frac{-x}{ \ln |x| + C } \) for \( 1 \le x \le 1.2\) explain why the value of \(y\) found in part (c) is greater than the approximate value of \(y\) found in part (a).
27. | A-Level |
(a) Express the following fraction in partial fractions.
$$ \frac{1}{F(5-3F)} $$The popularity of a student rock group is measured during their first year of gigs. The number of fans is modelled by the differential equation:
$$ \frac{dF}{dt} = \frac{F}{15} (5-3F) \quad 0 \le t \le 12 $$where F, in hundreds, is the number of fans and t is the time measured in months since the band began performing regularly.
(b) Given that there were 100 fans when the measurements began, determine the time taken, in months, for the number of fans to increase by 50%.
(c) Show that:
$$ F= \frac{A}{B+C^{-\frac{t}{3}}} $$where A, B and C are integers to be found.
28. | IB Analysis and Approaches |
Consider the differential equation \(x^2\dfrac{dy}{dx}=xy+y^2\). It is given that \(y = 2\), when \(x = 1\).
(a) Use Euler's method, with a step length of 0.1, to find an approximate value of \(y\) when \(x = 1.5\).
(b) Use the substitution \(y = vx\) to show that \(x\dfrac{dv}{dx}=v^2\)
.(c) By solving the differential equation, show that \(y = \dfrac{2x}{1-\ln{x^2}}\).
(d) Find the actual value of \(y\) when \(x = 1.5\).
(e) Using the graph of \(y = \dfrac{2x}{1-\ln{x^2}}\), suggest a reason why the approximation given by Euler's method in part (a) is not a good estimate to the actual value of \(y\) at x = \(1.5\).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
